定義（読み）ていぎ（英語表記）definition

日本大百科全書(ニッポニカ)

定義
ていぎ
definition

議論をする際に用いる概念（あるいは術語）の正確な意味づけを、その概念（あるいは術語）の定義という。たとえば、幾何学における円は、「平面上の一つの定まった点から、一定の距離にある点の全体」と定義される。定義の方法はこのように自然言語を用いて行われるのが普通であるが、数学では集合概念を用いたり、帰納的定義によったりすることも多い。たとえば、平面上に座標系が導入されていれば、点O=(a,b)を中心とする半径rの円は、集合｛(x,y)|(x-a)²+(y-b)²=r²｝と表すことができるから、円とは「ある点(a,b)と、ある正の実数rについての集合｛(x,y)|(x-a)²+(y-b)²=r²｝」と定義することもできる。また、フィボナッチ数列｛F(n)｝(1,1,2,3,5,8,13,……)を定めるとき、自然数上の関数F(n)について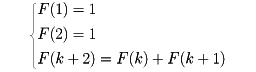

を用いて定義する例のように、数学的帰納法を用いて定義することもある。このような定義が帰納的定義である。

　定義は、厳密にはある議論のなかでの約束ごとであって、その議論のなかだけで通用するものである。したがって、議論の進め方によって同じ命題が定義になることも定理になることもある。

［廣瀬　健］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

定義
ていぎ
definition

言葉や物，事象をほかの言葉，物，事象で規定し，説明すること。定義される対象を被定義項という。被定義項が言葉であるか物であるかによって定義は名目定義と実質定義に大別される。手続の点からいえば，定義項に対しより短いか，より適切な被定義項を代入する短縮定義，被定義項に意味を述語づける意味論的定義 (「五角形は5辺をもつ多角形である」など) ，具体的対象に名詞を帰する直示定義などに分れる。また定義づけに伴う判断が分析か総合かによって分析的定義と総合的定義に分けられる。また定義は十全な規定でなくてはならない。アリストテレスは定義を言い替えや説明でなく対象の本質規定と考えていた。なお，中国では孔子や諸子百家が名実一致の理想を求めて正しく定義することを正名と呼んで重視した。

定義
じょうげ

宮城県中部，広瀬川の支流大倉川の段丘上にある地区。仙台市 (旧宮城町) に属する。定義如来のある極楽山西方寺の小門前町で，後白髪山 (1423m) の登山基地。素朴さを残す定義温泉が北方 2kmの山麓にある。

出典　ブリタニカ国際大百科事典 小項目事典

精選版 日本国語大辞典

てい‐ぎ【定義】

〘名〙 (definition の訳語) 概念の内容や用語の意味を正確に限定すること。また、その命題や式。

※百学連環（1870‐71頃）〈西周〉総論「而して其学に定義と云ふあり」

※吾輩は猫である（1905‐06）〈夏目漱石〉六「あの定義に合った様な理想的な円や直線は現実世界にはないもんです」

出典　精選版 日本国語大辞典

デジタル大辞泉

てい‐ぎ【定義】

［名］(スル)
１ 物事の意味・内容を他と区別できるように、言葉で明確に限定すること。「敬語の用法を定義する」
２ 論理学で、概念の内包を明瞭にし、その外延を確定すること。通常、その概念が属する最も近い類と種差を挙げることによってできる。
[類語]語義・意味・意義・意い・義ぎ・概念・謂いい・こころ・語意・字義・文意・含意・含み・意味合い・旨・ニュアンス・語感・本義・広義・狭義・原義・同義・異義

出典　小学館

世界大百科事典 第２版

ていぎ【定義 definition】

一般に用語の意味を明確に規定する文章(式を含んでもよい)を定義という。例えば，〈4頂角がすべて直角である四辺形を長方形という〉は長方形という用語に対する定義である。このとき，長方形の定義という言い方をする。なお，数学の理論建設にあたって，公理系を定めるが，そのときに定義をしない用語を用いることがある。通常，幾何の公理的方法での点，直線などがその例である。そのような用語を無定義用語，または無定義術語という。

出典　株式会社平凡社

普及版 字通

【定義】ていぎ

事物の概念を規定すること。

字通「定」の項目を見る。

出典　平凡社「普及版 字通」

世界大百科事典内の定義の言及

【幾何学基礎論】より

…図形は直観的に認識されるものであるが，直観はしばしば客観性を欠くので，明確にいい表された定義や公理の上に，直観を排して厳正な証明によって一貫した論理体系としての幾何学を構成しようという思想である。《ストイケイア》は，まず点，直線，円などの定義definitionを述べ，続いて〈任意の2点は直線で結べる〉のような図形についての五つの基本性質を公準postulateとしてあげ，また〈同じものに等しいものは互いに相等しい〉のような量の相等についての九つの基本事項を公理axiomとしてあげる。そして，これらの定義，公準，公理より出発して順次に論理的推論によって，直観的知見を定理として導き出す。…

【幾何学基礎論】より

…この著作は，古くから知られていた図形についての多くの知見を集大成して一つの学問体系にまとめあげたものであるが，これはプラトンによる次の思想の上に成立している。図形は直観的に認識されるものであるが，直観はしばしば客観性を欠くので，明確にいい表された定義や公理の上に，直観を排して厳正な証明によって一貫した論理体系としての幾何学を構成しようという思想である。《ストイケイア》は，まず点，直線，円などの定義definitionを述べ，続いて〈任意の2点は直線で結べる〉のような図形についての五つの基本性質を公準postulateとしてあげ，また〈同じものに等しいものは互いに相等しい〉のような量の相等についての九つの基本事項を公理axiomとしてあげる。…

※「定義」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社