翻訳|polygon
精選版 日本国語大辞典 「多角形」の意味・読み・例文・類語
たかっ‐けい タカク‥【多角形】
たかく‐けい【多角形】
出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報
改訂新版 世界大百科事典 「多角形」の意味・わかりやすい解説
多角形 (たかくけい)
polygon
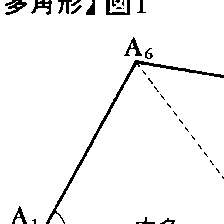
平面上に異なるn個の点A1,A2,……,Anがあって,線分A1A2,A2A3,……,An-1An,AnA1のどの二つの交点もA1,A2,……,Anのいずれかであるとき,これらn個の線分の作る図形をn角形A1A2……An,またはn辺形A1A2……Anといい,A1,A2,……,Anをその頂点,A1A2,A2A3,……,An-1An,AnA1をその辺という。n角形(n≧3)を総称して多角形という。多角形は平面を二つの部分に分け,そのうちの一方は有限の広がりをもつ。これを多角形の内部といい,多角形とその内部を合わせた図形もまた多角形と呼ばれる。多角形の各頂点Aiに対し,Aiを端点にもつ二つの辺が多角形の内部で作る角を内角といい,∠Aiで表す。どの内角も2直角を超えない多角形を凸多角形といい(図1),そうでないものを凹多角形という(図2)。凸多角形ではその内部に2点P,Qをとるとき,線分PQは内部に含まれる。内角が2直角以下のときその補角を外角という。多角形の相隣らない2頂点を結ぶ線分を対角線という。n角形はn(n-3)/2個の対角線をもつ。n角形はその内部にある適当な(n-3)個の対角線によって(n-2)個の三角形に分割され,したがってn角形のすべての内角の和は(2n-4)直角である。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「多角形」の意味・わかりやすい解説
多角形
たかくけい
polygon
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
日本大百科全書(ニッポニカ) 「多角形」の意味・わかりやすい解説
多角形
たかくけい
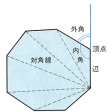
いくつかの線分で囲まれた平面図形をいう。その線分を多角形の辺といい、隣り合う線分の共通の端点を多角形の頂点という。多角形を多辺形ともいう。多角形の辺の個数がnのとき、頂点の個数もnで、このときn角形あるいはn辺形という。多角形の頂点を結ぶ線分で辺でないものを対角線というが、n角形の対角線はn(n-3)/2個ある。多角形の辺によって平面は多角形の内部と外部とに分けられるが、各頂点で二辺のなす角のうち内部にあるほうを多角形の内角という。n角形のn個の内角の和はその形にかかわらず180(n-2)度である。多角形のどの辺を延長しても多角形がその直線の一方の側にあるとき、凸(とつ)多角形という。凸多角形ではない多角形を凹(おう)多角形という。凸多角形ではn個の頂角のそれぞれの補角の和は一定で360度である。凹多角形で頂点において交互に凹凸ができている多角形を星形多角形という。多角形ですべての辺が等しい多角形を等辺多角形、すべての内角が等しい多角形を等角多角形という。等辺かつ等角である多角形が正多角形である。
[柴田敏男]
百科事典マイペディア 「多角形」の意味・わかりやすい解説
多角形【たかくけい】
→関連項目正多面体
出典 株式会社平凡社百科事典マイペディアについて 情報
お知らせ
4/12 日本大百科全書(ニッポニカ)を更新
4/12 デジタル大辞泉を更新
4/12 デジタル大辞泉プラスを更新
3/11 日本大百科全書(ニッポニカ)を更新
2/13 日本大百科全書(ニッポニカ)を更新