翻訳|vortex
精選版 日本国語大辞典 「渦」の意味・読み・例文・類語
うずうづ【渦】
- 〘 名詞 〙
- ① らせん状に巻きめぐる水の流れ。うずまき。
- [初出の実例]「絞水(うづ)の淵あり。故(かれ)、宇頭川と号(なづ)く」(出典:播磨風土記(715頃)揖保)
- ② 巻き込まれるような、激しい感情、熱気などが入り乱れている状態。また、入り乱れて混乱している状態。
- [初出の実例]「夜迄俗事の渦の中に立たるる翁にして」(出典:消息(1899‐1900)〈正岡子規〉)
- ③ ①の形をした模様。うずまき。
- [初出の実例]「天保前、渦は黒糸今は紺糸を流布とす」(出典:随筆・守貞漫稿(1837‐53)一三)
- ④ 丸い板を回し、吹き矢で吹き当てた場所の物品を得る遊び。主として子供の遊びであるが、賭博にも用いられた。
- [初出の実例]「辻番はうづをおい目にはって居る」(出典:雑俳・柳多留‐一九(1784))
- ⑤ 華道の花留の一つ。鉛の細板を渦巻状にしたもの。観世渦。
- ⑥ 「うずわがつお(渦輪鰹)」の略。
- ⑦ 魚「いさき(伊佐木)」の異名。〔和訓栞(1777‐1862)〕
改訂新版 世界大百科事典 「渦」の意味・わかりやすい解説
渦 (うず)
vortex
橋の上から川の流れを見ると,橋脚の後ろでは流れが渦を巻いていることがある。もっと身近にも,風呂の栓を抜いたときに排水口のまわりに渦ができるのはよく知られている。台風や竜巻は空気の渦であり,鳴門の渦巻は名所にまでなっている。このように見てくると,渦というのは水や空気などの流体が,円を描いて運動している状態といえそうである。私たちが日常的に渦という場合はこれで十分なのであるが,流体力学では流れが円を描いているだけではだめで,流体内の微小部分をとったとき,その部分がこまのように自転している場合にその部分には渦があるという。
流体の自転運動
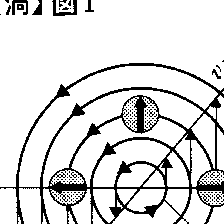
水を入れたバケツを鉛直軸のまわりに一定の角速度Ωで回転させると,やがて流体の各部が一定の方向に一定の角速度Ωで回転する状態に落ち着く。今,中心Oからrの距離にある水の微小部分Pについてその運動を考えてみよう(図1)。Pは速度v=rΩでOのまわりに回転運動をしているのは当然であるが,さらに自身の軸のまわりに回転運動(自転)をしていることがわかる。そしてこの自転は,Oのまわりを1回公転する間にちょうど1回転しているから,自転の角速度はΩである。これはrのどの部分をとっても同じで,バケツの中の水はどの部分でもすべてΩの角速度で自転している。
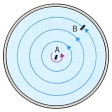
これに対して図2は風呂の栓を抜いたときに見られる渦である。図1と同じく流線は同心円状で水はどの部分をとっても等速円運動をしているが,その速度は中心のごく近くを除くと,中心から遠ざかるに従って遅くなっている。この場合には中心近くの水を除いては自転の角速度はきわめて小さい。したがって見た目には同じように見えても,バケツの渦とは性質が大きく異なっている。
このような流体の自転は,2枚の平行平板(距離h)の間に粘性のある流体をはさみ,一方の平板を一定の速度Uで動かしてやるときにも生じ,このときにはU/2hの角速度で回転する状態に落ち着く。
渦度
渦を特徴づけているのは流体の回転(自転)運動であり,この回転の角速度で渦の強さを表すことができる。流体のある部分が角速度Ωで回転しているとき,その部分はω=2Ωの渦度をもつという。先のバケツの例では流体はどの部分でも一様な渦度2Ωをもっており,また風呂の栓を抜いた場合では,中心ほど渦度が大きく,中心から遠ざかるに従って渦度は小さくなっている。渦度はベクトルであって,その方向は,回転軸の回転の向きに右ねじを回したとき,右ねじの進む方向にとるのが慣習である。一般の渦運動では流体の各点のまわりにこのような回転運動があり,ベクトルとしての渦度は場所ごとに変化する。粘性が小さく渦のない流れでも,その中におかれた物体の表面では流れが静止するために,流れに垂直な軸をもつ渦の集中した薄い層(境界層)が表面に存在する。このような渦層は速さの異なる二つの平行流の界面にも現れる。粘性が無視できて摩擦によるエネルギーの散逸がない完全流体では,外力が非回転力(保存力)であるような場合には,渦のない流体部分から新しく渦ができることはなく,またいったん生じた渦は決して消滅することはない。これをヘルムホルツの渦定理,またはラグランジュの渦定理という。しかし実際には,粘性のきわめて小さい流体でも,物体面に角があったり,流速がある限度を超過したりすると,境界層が物体面からはがれて流れの中に渦が現れることになる。自由な渦層は一般に不安定であって大小の渦が複雑に乱れた渦運動(乱流)に移行する。
渦線
流れのようすをわかりやすくするのに流線という概念が用いられるのと同じように,渦の運動には渦線が用いられる。流線は,接線の方向がその点における流れの方向を示す曲線であるが,渦線は,接線の方向がその点における渦度の方向と一致するような曲線である。
渦線の集りで,とくに直線あるいは曲線に沿って渦が集中したものを理想化して渦糸と呼ぶことがある。排水口の上部に見られる渦や竜巻はその一例である。渦度は渦糸に平行であり,そのすぐまわりの渦のない領域にある流体は渦糸を軸とする同心円上を半径に逆比例する誘導速度で運動する。この速度の大きさvと円周2πrとの積γ=2πrvは1本の渦糸に沿ってはどこでも一定であって,このγを渦糸の強さと呼ぶ。一般に渦糸から離れた任意の点での誘導速度は,γに等しい強さの電流が流れる同形の電線による磁場(ビオ=サバールの法則)と同一である。不生不滅の渦では渦がまわりの流れとともに流されていくとみなすことができる。そこで二つの平行な孤立直線渦をとれば,両者の強さの重心ともいうべき軸のまわりを円運動する。とくに流体中で円柱が急発進したときに見られるような向きが反対で強さが等しい1対の渦は渦対と呼ばれ,両者を結ぶ平面に垂直に併進運動する。円柱の速さが大きく,多数の渦が発生して渦列を作るときは,対称な配置のものは不安定で,交番して発生して互い違いに並ぶ。これをカルマン渦というが,さらに速度が大きいとこれもくずれて乱流となる。
曲がった渦糸の各部はまわりの流れのために伸び縮みし,動かされるが,とくに強くて細いときはその強さと曲率に比例した速度で接触面に垂直に動かされ,またそれに沿っての孤立波や振動の担い手になる。これに近いことはタバコの煙などに見られる円形の渦輪で実現されていて,面に垂直に一定速度で動くばかりでなく,同軸の二つの渦輪では相互作用のために先行するものの半径が増大して速度が遅くなり,後行のものは半径が短くなって速くなり,交互の追抜現象も可能となる。一般に渦糸は境界で終わるか,輪を作るかのいずれかであって,流体の中で切れることはない。
渦管
流れの中に閉曲線を考え,その上の各点を通って渦線を引くと一つの管ができる。これを渦管といい,これの細いものが渦糸である。したがって一般の渦管は渦糸が連続的に分布して束になったものとみなすことができ,その全体の強さを渦束ともいう。渦束はその断面に垂直な渦度の総和であるが,渦糸のときのように,それを一周する任意の閉曲線に沿って流速vsを積分したもの(循環γ=∫vsds)に等しく,その値は渦管に沿って一定である。したがって管が伸びて細くなると表面での回転速度は増加する。とくに完全流体では渦管が流れとともに動いていき,その強さは不変であるので,この効果が著しい。
渦の中の圧力
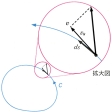
渦を見ると,その中心はじょうごのようにくぼんだ形をしている。円運動をしている流体の一部を考えると,この部分には求心力が作用していなければならないが,この力は考えている流体部分の両側の圧力差によって与えられる(図3)。流体中の1点の圧力は,その上にある流体の重量と大気圧の和として決まる。求心力が与えられるためには中心から遠ざかるほど流体の圧力は高くなっていなければならず,このために流体はじょうご形にくぼんでいなければならない。
渦に作用する力
いま左から右に流れる流れの中に,時計まわりの渦を固定しておくと,流れは下向きに偏向して運動量を得るので,その反作用として渦には上向きの力(揚力)が働く。円柱などの物体を回転させて流れの中におくとき,揚力が働くのも物体を渦とみなせばまったく同じことであり,これをマグヌス効果と呼ぶ。また流れの中におかれた翼形に働く揚力も,後縁での流れを滑らかにするように境界層がはがれ,反時計まわりの循環γをもった渦が放出されて流されていき,翼のまわりには時計まわりの強さγの循環が残るためと解釈できる。速度Vの定常な流れで,揚力の大きさが流体の密度をρとするとき,ρVγに等しいというのがクッタ=ジューコフスキーの定理である。このように揚力の働く翼は束縛された渦とみなすことができるが,翼端で切れることはできないので,流れに沿う後ひき渦として下流に伸び,運動開始時に放出され流されていく渦とつながってループを作っているものと考えることができる。この後ひき渦を核として水蒸気の凝縮したものが飛行機雲として見られるのである。粘性の大きな流体の場合は渦が集中せず拡散して分布し,流れの中の凹面や角のところで流線が壁から離れて循環流や渦の列を作ることがある。
地球や惑星のように回転している物体上の流体の運動は,恒常的に分布した渦が背景にあると考え,その地形上での運動やかく乱として考えれば理解できることが多い。また曲がった管や水路の中の流れに垂直な面内に誘起される流れ(二次流)も,粘性などによって生ずる流れに垂直な渦が水路の屈曲によって断面内の回転を誘発したと解釈することができる。分布した渦はこのほかにも,熱現象や化学反応など,また電流に働く力など非保存力のある場合にはよく見られる現象である。
執筆者:橋本 英典
大気や海洋の渦
地球の表面積の70.8%は海水で占められている。さらに大気が地球全体を覆っている。この地球上における巨大な流体,すなわち大気と海水はつねに運動しており,渦を伴っている。渦にはその特徴的なスケールが非常に小さいものから何千kmに及ぶものまでさまざまな形態で存在する。地球上の流体の運動のうち規模の小さなものでは,流体が地球とともに回転している影響を無視できる。しかし,運動の規模が大きければ,その流体が地球とともに回転している効果を無視できなくなり,海水や大気がたとえ完全流体であったとしても渦が生じうる。もちろん大気も海水も完全流体ではないので,前述の条件下で生ずる渦が多数あり,それらが回転の影響を受けて運動することになる。つまり大気や海水はつねに渦だらけともいえる状態にあり,この渦が大気や海水の運動に大きな影響を与えている。大気大循環,海洋大循環に密接な関係があるロスビー波(惑星波)は渦が伝播(でんぱ)しているものともいえるし,低気圧,台風,高気圧もまた渦から成り立っており,さらに小規模なものとしては竜巻,火事旋風などがある。また雲のカルマン渦も人工衛星からとらえられている。さらに大洋中の中規模渦,黒潮や湾流の蛇行に伴う冷水塊や暖水塊もそれぞれ冷水渦,暖水渦と呼ばれる渦である。
簡単のため地球上で密度一様な流体を考えると,地球とともに回転する座標系から見たその大規模運動の方程式は,摩擦や外力を無視して,近似的に,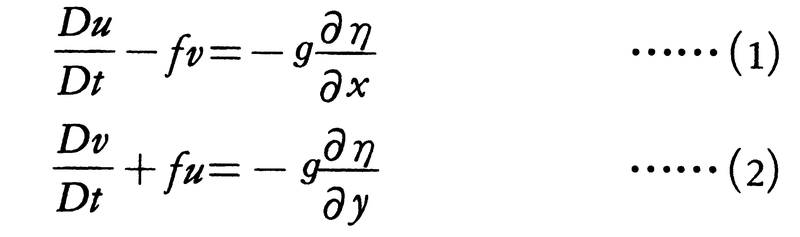
と書ける。ただし東向きにx座標を,北向きにy座標をとり,鉛直方向には静水圧を仮定した。上式中のηは流体面の変位,u,vはそれぞれ東向き,北向きの速度を表し,gは重力加速度,fはコリオリの力の鉛直成分(f=2Ωsin φ。ここでΩは地球の回転角速度(2π/d),φは緯度)であり,この場合地球が回転して効果が生みだしている渦の強さを表す量ともみなせる。また記号D/Dtは分質微分を表し次式で定義される。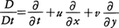
(1)(2)式からηを消去すると,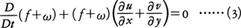
が得られる。ここでωは,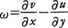 のことで流体自身がもつ渦度の鉛直成分を表している。地球の回転による渦度fを惑星渦度と呼ぶのに対しωを相対渦度と呼ぶ。(3)式は渦度方程式と呼ばれるが,注目すべきはfとωがつねに和の形で方程式に入っていることで,f+ωを絶対渦度という。(3)式から,最初(t=0),海水や大気自身に渦がない(ω=0)としても,時間が経過すれば(t>0)渦が発生する(ω≠0,つまりω>0かω<0)ことがわかる。
のことで流体自身がもつ渦度の鉛直成分を表している。地球の回転による渦度fを惑星渦度と呼ぶのに対しωを相対渦度と呼ぶ。(3)式は渦度方程式と呼ばれるが,注目すべきはfとωがつねに和の形で方程式に入っていることで,f+ωを絶対渦度という。(3)式から,最初(t=0),海水や大気自身に渦がない(ω=0)としても,時間が経過すれば(t>0)渦が発生する(ω≠0,つまりω>0かω<0)ことがわかる。
地球上の大規模な渦はその渦度の水平成分が鉛直成分に比べて無視できるのが大きな特徴である。いいかえれば渦管がつねに鉛直方向に向いたまま運動しているわけであるが,これは地球が回転しているためと,水平方向のスケールが鉛直方向のスケールに比べてきわめて大きいためである。
渦位
回転流体においては渦度よりも渦位(ポテンシャル渦度ともいう)のほうが便利な概念である。渦位とは流体中にある水柱を考え,その高さh+η(hは平均水位の高さ)で渦度のz成分を割った量である。密度が一様な完全流体においては絶対渦位(f+ω)/(h+η)が保存されることが示されるが,この性質はきわめて重要な保存則である。
執筆者:菊池 幸雄+宮田 元靖
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「渦」の意味・わかりやすい解説
渦
うず
vortex
流体(気体または液体)の一部がこまのように回転しているとき、その部分は渦運動をしているという。また、その部分を渦という。たとえば、鳴門(なると)の渦潮は大きな水の渦で、台風は空気の渦である。茶碗(ちゃわん)に入れた水をスプーンでかき回すと、茶碗の中の水全体がこまのように回転するので、水全体は一つの渦巻と考えることができるが、茶かすを浮かべて細かく観察すると、水の各部分はそれぞれ異なる回転運動をしていることがわかる。たとえば、中心付近の茶かすはぐるぐる回転するのに対して、中心を外れた茶かすはその姿勢を保ったまま円運動をする。すなわち、茶碗の中心付近の水の部分は自転をするのに、中心を外れた水の部分はほとんど自転をしない()。この自転をする水の部分が渦である。
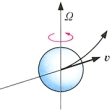
川の流れのように、一般に流体が運動する場合、流体全体としての運動はきわめて複雑であっても、その各部分を考えると比較的簡単である。すなわち、小さい球状の部分をとって考えると、それは自転しながら並進運動を行っている。その並進運動の速度vがその点での流れの速度である()。自転の角速度Ωの2倍ω=2Ωを流れの渦度(うずど)という。円筒形の容器に水を入れて、中心軸の周りに一定の角速度Ωで回転すると、やがて水は容器と一体となって回転する。このとき、中心から半径rのところの水はv=Ωrの速度で円運動をする。このとき
流速×円周=2πΩr2
=渦度×円の面積
の関係がある。この場合、水の各部分は同じ自転の角速度Ω、したがって渦度ω=2Ωをもつので、それに面積を掛けた前式の右辺は、半径rの円に含まれる渦の総量を表すと考えられる。これを渦の強さという。一方、「流速×円周」は円周に沿う循環とよばれる。一般に、任意の閉曲線Cについて、流速の接線成分vsとCの線要素dsとの積vsdsを加え合わせた量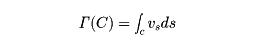
を、Cに沿う循環といい、
Γ(C)=Cに含まれる渦の総量
という関係がある()。流れの中の流体の微小部分(これを流体粒子という)をとると、ある回転角速度Ωで自転しながら、ある速度vで並進運動をしている。その自転軸の方向に近接した流体粒子をとると、それはまたある角速度で自転している。このように次々と自転軸をつなぎ合わせていくと、流体粒子は数珠(じゅず)玉のようにつながって、流体の細い紐(ひも)ができる()。これを渦糸(うずいと)という。また、数珠糸に相当する曲線を渦線(うずせん)という。つまり、渦線は自転軸を連ねてできる曲線で、その曲線を軸として流体が回転運動をしていることを示す。いま、一つの小さい閉曲線上の各点を通る渦線を考えると、渦線を壁とする管ができる。これを渦管(うずくだ)という。渦管の任意の点での断面積σと渦度の大きさωとの積Γ=ωσは一定で、渦管の強さとよばれる。渦管の細いところでは流体の回転は速く、太いところでは遅い。竜巻やつむじ風は、近似的に1本の渦管のように考えられるが、地面に近いところでは回転は遅く、地面から離れて細くなったところでは回転が速い。細い渦管に含まれる流体の部分が、すなわち前述の渦糸である。
[今井 功]
渦糸の性質目次を見る
空気や水のような流体は粘性が小さい。粘性がまったくないような流体を完全流体という。完全流体の中では渦は新たに発生することもなく、またいったん発生した渦はいつまでも消滅することはない。これをラグランジュの渦定理という。完全流体の中の渦糸は時々刻々に変形しながら流れにのって運動するが、その強さΓ=ωσはいつまでも変わらない。伸びると断面積が減って自転の角速度を増す。渦糸は流れの中で中断することはなく、流れの境界から境界まで伸びているか、あるいは閉曲線をつくるかのいずれかである。後者を渦輪(うずわ)という。たばこの煙の輪は渦輪の一例である。閉曲線Cに沿っての循環Γ(C)はCを貫く渦糸の強さの総和を表すから、完全流体ではラグランジュの渦定理により、流体に固定した閉曲線に沿っての循環は時間的に一定不変である。これをケルビンの循環定理という。
[今井 功]
渦の発生目次を見る
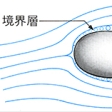
物体に流れが当たる場合、粘性のために流速は物体表面の薄い層の中で急にゼロまで下がる。この薄い層は境界層boundary layerとよばれ、静止した物体と流れる流体に挟まれて回転する、ころの役割を演じる()。これは自転する流体として渦の一種である。つまり境界層は渦の層である。境界層が物体表面からはがれて流れの中に押し出していって分裂すると大小さまざまな渦ができる。
[今井 功]
渦の量子化目次を見る
液体ヘリウムは絶対温度2.2K以下の極低温では超流動性をもつ。超流動流体では量子効果が現れ、ケルビンの循環定理は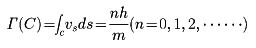
の形になる。ただし、hはプランク定数、mはヘリウム原子の質量である。このように循環は量子化されてとびとびの値をとる。循環は閉曲線を貫く渦糸の強さにほかならないから、これは渦の量子化を意味する。液体ヘリウムの中にイオンを打ち込むとき、イオンによって小さい渦輪がつくられるが、その強さΓが前の式のn=1で与えられることが実験的に証明された。これは、液体の運動というマクロの現象にも量子的効果が現れることを示すものとして重要である。
[今井 功]
ブリタニカ国際大百科事典 小項目事典 「渦」の意味・わかりやすい解説
渦
うず
vortex
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
普及版 字通 「渦」の読み・字形・画数・意味
渦
常用漢字 12画
[字訓] うず
[字形] 形声
声符は咼(か)。咼は
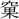 と声義近く、まるくくぼんだ形のものをいう。水がはげしく渦まくとき、その形となる。
と声義近く、まるくくぼんだ形のものをいう。水がはげしく渦まくとき、その形となる。[訓義]
1. うず、うずまく。
[熟語]
渦水▶・渦旋▶・渦中▶・渦盤▶
[下接語]
水渦・清渦・千渦・旋渦・白渦・微渦・瑶渦
出典 平凡社「普及版 字通」普及版 字通について 情報
百科事典マイペディア 「渦」の意味・わかりやすい解説
渦【うず】
出典 株式会社平凡社百科事典マイペディアについて 情報
化学辞典 第2版 「渦」の解説
渦
ウズ
vortex
流体中における流体要素の回転運動,あるいはその回転運動している部分をいう.流体のなかに種々の渦が不規則に存在するようになった流れを乱流という.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
デジタル大辞泉プラス 「渦」の解説
渦〔戯曲〕
渦〔小説〕
世界大百科事典(旧版)内の渦の言及
【冷水塊】より
…海洋中に存在する周囲より低温の海水の塊。普通直径100~200kmくらいの円形状をなし回転運動を伴っており,冷水渦ともいう。海水はいたるところ均質ではなく,場所により異なった性質の海水が入り乱れているのが普通である。…
※「渦」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
貨幣 (名目) 賃金額を消費者物価指数でデフレートしたもので,基準時に比較した賃金の購買力を計測するために用いられる。こうしたとらえ方は,名目賃金の上昇が物価の上昇によって実質的には減価させられている...

 〈カ〉
〈カ〉 〈うず〉「
〈うず〉「