精選版 日本国語大辞典 「ダランベールの原理」の意味・読み・例文・類語
ダランベール の 原理(げんり)
出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報
出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報
静力学における仮想変位の原理を動力学に拡張したもので,1743年にJ.L.R.ダランベールによって述べられた。ニュートンの運動法則は各質点の質量をmi,位置をxi,作用する力をFiとして,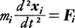 と書かれるが,これを,
と書かれるが,これを,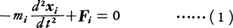
と書いてみると,(1)は,質点系の各質点に働く力がすべて0になるという静止の条件,Fi=0におけるFiを,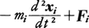 で置き換えたものになっている。このことに着目すると,仮想変位δxi(運動方程式に従って生ずる変位とは無関係で束縛条件の許す範囲でまったく任意)に対し仕事をなす力を,
で置き換えたものになっている。このことに着目すると,仮想変位δxi(運動方程式に従って生ずる変位とは無関係で束縛条件の許す範囲でまったく任意)に対し仕事をなす力を,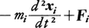 とすることにより,運動方程式(1)そのものが導かれることになる。この場合,
とすることにより,運動方程式(1)そのものが導かれることになる。この場合,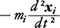 を質点iに働く力の一種とみなし慣性力または慣性抵抗と呼ぶ。その結果,質点系の運動は各質点に働く慣性力まで含めた力のなす仮想仕事δWの総和が各時刻でつねに0,すなわち,
を質点iに働く力の一種とみなし慣性力または慣性抵抗と呼ぶ。その結果,質点系の運動は各質点に働く慣性力まで含めた力のなす仮想仕事δWの総和が各時刻でつねに0,すなわち,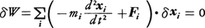 という条件に従うように定まる。同様に剛体系の運動に対しては,各剛体(質量Mi)の重心xigの並進運動に関し,
という条件に従うように定まる。同様に剛体系の運動に対しては,各剛体(質量Mi)の重心xigの並進運動に関し,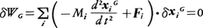
また,各重心のまわりの回転ωi(回転軸方向大きさ回転角のベクトル)に関し,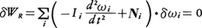
で表されることになる(Iiは剛体iの慣性モーメント,Niは剛体iに働く力のモーメント)。以上がダランベールの原理の実質的内容で,同時代の最小作用の原理とともに力学の変分原理の先駆けとなった。
→変分原理
執筆者:長谷川 洋
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
フランスの物理学者・数学者・哲学者ダランベールが導入した力学の原理の一つ。力の作用の下で加速度運動をしている物体の運動を、ある仮想的な力を考えることによって、それらの力がつり合って平衡状態にあるとして静力学的に取り扱うことができることを述べた原理。物体の質量をm、働いている力をF、加速度をaとすると、ニュートンの運動方程式はF-ma=0と書き換えることができる。このように書いたときの-maを一種の仮想的な力とみなすと、左辺は物体に働く力の合成を表しており、その合成した力が0になるということによってつり合いの条件となっている。内容としてはニュートンの運動方程式と同じであるが、運動している物体の動力学の問題を、静力学の問題に帰着させたことになる。ただし、ここでいうつり合いは、運動の各瞬間ごとに変化していく力の間に成立しているものである。具体的な例として、急に加速された車に乗っている人が、後ろのシートに押し付けられるように感じる場合を考える。これは本当に何かの力で押さえ付けられるのではなく、加速される前の状態を維持しようとする慣性のために体が取り残される結果おこるのである。このとき、シートが体を前に押す力と慣性による仮想的力がつり合っている結果、体がシートの上に静止しているとみるのがこの原理の意味するところである。この意味で-maのことを慣性抵抗または慣性力とよんでいる。また、本当に働いている力ではないという意味で見かけの力とよぶこともある。この種の力の例として、等速円運動をしている物体に関する遠心力がある。ダランベールの原理は、つり合いの条件を決定する仮想仕事の原理の形にいいかえて、力学法則の解析的な展開、すなわち解析力学の体系化のための有用な手段となった。
[永田 忍]
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
出典 株式会社平凡社百科事典マイペディアについて 情報
…1739年,最初の数学論文を公表したあと,つぎつぎに業績を発表し,41年23歳でアカデミー・デ・シアンス準会員補,68年幾何学年金受領会員となる。1743年《動力学論》を発表し,質点が加速度をもつ場合でも,慣性抵抗を含めて力のつりあいを考えれば動力学を静力学に還元できるという〈ダランベールの原理〉を展開した。翌年その続編《液体の均衡と運動論》を出し,46年には《風の一般理論》によってプロイセン・アカデミー賞を獲得,同時にその会員に選出された。…
※「ダランベールの原理」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
4/12 日本大百科全書(ニッポニカ)を更新
4/12 デジタル大辞泉を更新
4/12 デジタル大辞泉プラスを更新
3/11 日本大百科全書(ニッポニカ)を更新
2/13 日本大百科全書(ニッポニカ)を更新