精選版 日本国語大辞典 「運動方程式」の意味・読み・例文・類語
うんどう‐ほうていしき ‥ハウテイシキ【運動方程式】
出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報
出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報
外力の作用のもとでの物体の運動を決めるための方程式。数学的には微分方程式の形をとる。各種のものがあるが,以下に代表的なものを示す。
(1)ニュートンの運動方程式 運動の変化(加速度)は力の作用に比例し,その方向に起こるというニュートンの運動の第2法則を数式的に表した,
ma=F ……(1)
または,
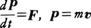 ……(1)′
……(1)′
を指す。ただしmは物体の質量,v,aはそれぞれの速度ベクトル,加速度ベクトルであり,またpは運動量ベクトル,Fは物体に働く力を表す。力Fが一般に位置r,速度vおよび時間tなどの関数としてわかっていれば,ある時刻,例えばt=0の位置と速度を知ることによって,それ以後の物体の運動は運動方程式から完全に(すなわち物体の位置rを時間tの関数として)知ることができる。
(2)剛体の運動方程式 (1)の方程式は,物体が回転運動をしているときは質量の中心(重心)の運動についてだけあてはまる。回転運動そのものについては(1)を基礎にして回転体の運動方程式を導き,それを解かねばならない。いま剛体がある固定軸のまわりに回転しているとしよう。剛体を多くの微小な部分に分け,i番目の部分の質量をmi,回転軸からの距離をriとする。この部分は半径riの円周上を運動する。そこに働く力の円周方向の成分をfiとすると,回転角速度ωの時間的変化率(角加速度)\(\frac{dω}{dt}\)は,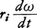 が円周方向の加速度だから,(1)式により
が円周方向の加速度だから,(1)式により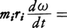
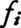 を満たす。この両辺にriを掛け,iについて加え合わせる。
を満たす。この両辺にriを掛け,iについて加え合わせる。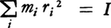 は,回転軸のまわりの慣性モーメントに等しく,
は,回転軸のまわりの慣性モーメントに等しく,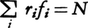 とすると,この和で剛体の微小部分の間に働いている力からの寄与は,作用反作用の法則のため打ち消し合うので,Nとしては剛体に働く外力のモーメントだけが残ることになる。したがって回転運動を決める運動方程式は,
とすると,この和で剛体の微小部分の間に働いている力からの寄与は,作用反作用の法則のため打ち消し合うので,Nとしては剛体に働く外力のモーメントだけが残ることになる。したがって回転運動を決める運動方程式は,

の形となる。L=Iωは軸のまわりの角運動量であるから,(2)を,
のように書くこともできる。1点を固定した剛体の回転運動は,瞬間的に三つの座標軸Ox,Oy,Ozのまわりの回転運動を合わせたものと見なせるので,剛体の角運動量も力のモーメントもベクトルL,Nに置き換えて運動方程式として,

を得る。回転運動を剛体に固定した座標系,とくに慣性の主軸に選んでやれば,(2)″はオイラーの方程式と呼ばれるものになる。
→回転運動
(3)流体の運動方程式 流体の場合も,その微小部分に着目することによって,(1)の運動方程式から流体に対するラグランジュの運動方程式またはオイラーの運動方程式を導くことができる。両者の差異は流体の運動の記述のしかたの違いにより,前者では流体の微小部分の運動を追究し,また後者では各瞬間における流体各点での速度,圧力,密度の値,すなわちこれらの量の場を求める。
(4)相対論的運動方程式 (1)′において,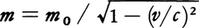 (m0は静止質量)
(m0は静止質量)
としたものが相対論による修正を受けた運動方程式である。
→相対性理論
(5)解析力学の運動方程式 解析力学では,体系の自由度に応じて適宜に選ぶ,一般化された座標(q1,q2,……,qf)=qを用いた場合に便利なラグランジュの運動方程式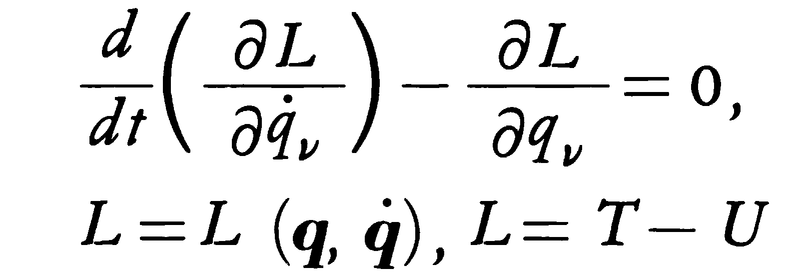
(qはdq/dtを表し,Lはラグランジュ関数,T,Uはそれぞれ運動エネルギーおよび位置エネルギーである)
およびハミルトンの正準方程式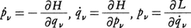
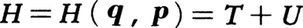 (pνはqνに共役な運動量,Hはハミルトン関数)
(pνはqνに共役な運動量,Hはハミルトン関数)
などが現れるが,これらもニュートンの運動方程式をもとにして導かれることに変りはない。
→解析力学
(6)量子力学の運動方程式 量子力学でも見かけは(1)とまったく同じ形のハイゼンベルクの運動方程式が現れる。しかしこの場合,実は位置や運動量が積の交換律を満たさない量子力学的な量になっているので扱いはそれほど簡単でない。むしろ内容的にはまったく等価な,波動関数とシュレーディンガー方程式を用いるやり方のほうがわかりやすく,ふつうに行われている。それによると,量子力学では保存力Fについて両辺の期待値をとった形で(1)の運動方程式がなりたつことが示される。
→運動
執筆者:田辺 行人
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
物理における物体の運動を理解するための方程式。歴史的にはニュートンの運動の第二法則により、最初のニュートンの運動方程式がF=maという形で提案された。ここでFは力、mは質量、aは加速度である。その後、流体力学に対するオイラー方程式、ナビエ‐ストークス方程式も提案される。しかし、重力のような中心力を扱う場合に便利な極座標系で運動方程式を扱うと、方程式が複雑になる。そこで座標系に依存しない形での運動方程式を研究した結果、解析力学としてラグランジュの運動方程式、ハミルトンの正準運動方程式に発展した。量子力学の発展期には、ハミルトン形式の運動方程式からハイゼンベルクの運動方程式が開発された。
[山本将史 2021年7月16日]
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
血液中の脂質(トリグリセリド、コレステロールなど)濃度が基準値の範囲内にない状態(脂質異常症)に対し用いられる薬剤。スタチン(HMG-CoA還元酵素阻害薬)、PCSK9阻害薬、MTP阻害薬、レジン(陰...
4/12 日本大百科全書(ニッポニカ)を更新
4/12 デジタル大辞泉を更新
4/12 デジタル大辞泉プラスを更新
3/11 日本大百科全書(ニッポニカ)を更新
2/13 日本大百科全書(ニッポニカ)を更新