改訂新版 世界大百科事典 「解析力学」の意味・わかりやすい解説
解析力学 (かいせきりきがく)
analytical mechanics
物理学の一分野。ニュートンの3法則に基づく力学を,個々の実例を離れたより一般的な形式にまとめたもの。18世紀後半から19世紀にかけてJ.ラグランジュ,W.ハミルトン,K.ヤコービらによって展開,確立され,相対性理論,統計力学,量子力学に対しそれらの理論構成に基本的な寄与を果たした。
力学系の自由度と一般化座標
簡単な例として,質量m,電荷eの1個の荷電粒子に対する運動方程式,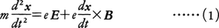
を考えると(xは粒子の位置ベクトル,tは時間,Eは電場,Bは磁場),これは粒子が電磁場(E,B)の力を受けて一定の初期条件のもとに空間の中で描く軌道を決定する。この場合,この力学系の自由度fは空間の次元数3である。もっと一般にn個の粒子に対し同様な運動方程式がたてられればf=3nであり,またこれらの座標間に一定の関係,例えばh個の式gν(x1,……,xn)=0が運動方程式と独立に成立している場合(これを束縛条件という),自由度はf=3n-hとなる。そして粒子の位置座標は必ずしも直交座標系に限られる必要はなく,各質点の直交座標の代りにそれらを互いに独立なf個の関数によって,q1,q2,……,qfで体系の配置を表してもよい。このq1,q2,……,qfを一般化座標と呼び,一般化座標を用いて論ぜられるのが解析力学の特徴である。
→座標
正準運動方程式
現代の物理でいう力学系とは広義概念の運動方程式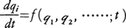 に従う体系を指すことが多いが,解析力学ではその特別な場合,すなわち時間の2階常微分方程式を備えている場合に限定される。(1)において右辺の電磁場が時間変数tを座標を通して以外直接含まぬ場合(このとき(1)の力学系は自律系と呼ばれる),tを-tに,Bを-Bに変えても方程式は不変である。これは時間反転の特性と呼ばれ,解析力学の扱う対象が第一義的には可逆現象に限定されることを意味する。常微分方程式論により高階の微分方程式は変数を増して階数を減らすことができるはずであり,一般化座標q1……qfの力学系に対して次のような運動方程式が設定される。
に従う体系を指すことが多いが,解析力学ではその特別な場合,すなわち時間の2階常微分方程式を備えている場合に限定される。(1)において右辺の電磁場が時間変数tを座標を通して以外直接含まぬ場合(このとき(1)の力学系は自律系と呼ばれる),tを-tに,Bを-Bに変えても方程式は不変である。これは時間反転の特性と呼ばれ,解析力学の扱う対象が第一義的には可逆現象に限定されることを意味する。常微分方程式論により高階の微分方程式は変数を増して階数を減らすことができるはずであり,一般化座標q1……qfの力学系に対して次のような運動方程式が設定される。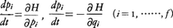

ここでqiに対しpiをその共役運動量,両者を合わせて正準変数と呼ぶ。このように2f個の1階常微分方程式に従い,しかもこの常微分方程式が単一のスカラー関数H(p1,……,pf,q1,……,qf;t)(Hはハミルトン関数)から導かれている場合が解析力学の対象とする力学系の運動の標準形であって,この方程式は正準運動方程式と呼ばれる。荷電粒子の例でいうならば,ベクトルポテンシャルA,スカラーポテンシャルφによって,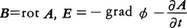
と表すことにより,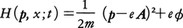
から(1)が導かれる。非相対論の場合Hは一般的に正準運動量の二次形式で書かれ,したがって正準座標の速度と運動量との間の一次関係で正準方程式(2)の前半が尽くされる。正準形式の重要な点は(2)の構造が相対論にももち越されることで,上例で,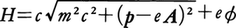
とすることで確かめられる(cは光速度)。
相空間
正準変数q1,……,qf;p1,……,pfの作る2f次元ユークリッド空間を相空間または位相空間phase spaceといい,(2)の解はこの空間における軌道群(異なる軌道は異なる初期値に対応)で表されるが,次のような基本的性質が備わっている。
(1)体積不変性 体積Vの任意の領域を取り,その中の点すべてを(2)に従って追跡したとき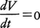
(2)密度不変性 (2)に従う力学系の集団を考え,密度関数ρ(t,p,q)によって分布しているものとすると,上と同じ領域に出入りする(状態)点の総和はつねに0に保たれる。
これは可逆的な運動法則のみによって建設される統計力学の基礎事項である。自然現象には不可逆過程と呼ばれる(2)に含まれない型の運動も重要であるが,これはたくさんの自由度の(2)型の力学系から巨視変数以外の不必要な自由度の変数を消去することにより,運動が相空間の部分空間に制限されたものと考えられる。
正準変換
(2)の運動を変数の変換qi=qi(Q,P),pi=pi(Q,P)によって新変数(Qi,Pi)i=1,......,fで記述する場合,方程式の形が同じならば運動法則の記述はこの変換によって不変であり,系の力学的性質の理解は統一されたものになる。厳密な定式化では微分形式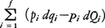
(pidqi-PidQi)がスカラー関数W(q,Q;t)の全微分になるとき,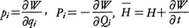
によって新正準変数(Q,P)が定義され,新ハミルトン関数H(P,Q)を用いて(2)と同じ正準方程式となる。これをW(q,Q;t)を母関数とする正準変換という。
ポアソン括弧式
二つの関数u(q,p),v(q,p)に対し定義される量,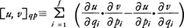
をポアソン括弧式という。これは正準変換の不変式で,これにより正準変換の条件が[Qi,Qj]=[Pi,Pj]=0,[Qi,Pj]=δijとなる。また正準運動方程式(2)は,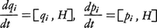
と表される。1920年代量子力学の定式化は,非可換量(行列)で表される物理量の運動が同様な形式に従うという認識から始められた。
執筆者:長谷川 洋
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「解析力学」の意味・わかりやすい解説
解析力学
かいせきりきがく
力学の基本法則すなわち運動の法則に基づいて物体の運動を広く理解することを目的として体系化された物理学の一分科で、多くは数学的な形式をとっている。
ニュートンの力学は、質点が力の作用を受けたとき、どのようにその運動量(速度×質量)が変わるかを与える。ニュートンは、その法則を彼の有名な著作『プリンキピア』のなかで詳しく述べたが、その叙述の方法は幾何学的であった。ニュートンの運動の法則から出発すると、質点の集まりである質点系に対してだけでなく、剛体や弾性体・流体などの連続体をも質点が無限個集まった系とみなすことによって、これらの系の運動方程式を導くことができる。その結果、質点と質点系および連続体のいずれの力学的な運動をも対象とする一般的な力学の体系ができあがってきた。『プリンキピア』と異なり、この一般的な力学の体系では、微分積分学の手法をおもに用いているため、解析力学とよばれている。電磁気学の法則も解析力学の運動方程式に書き換えることができるので、解析力学の完成は、ニュートンの運動の法則の単なる数学的一般化ではなく、質点と連続体および電磁場に対する一般的な法則の発見につながるものである。実際、解析力学の理論の形成には、光の伝播(でんぱ)の理論の形式が用いられている。
[田中 一]
一般化座標と運動量
質点の速度に質量を掛けたものを運動量といい、pで表すことが多い。ニュートンの運動の第二法則、すなわち、質点の加速度に質点の質量を掛けたものが、外から加える力fに等しいという運動法則を、質点の座標xと運動量pで書き表せば、運動の第二法則は、質点の質量をまったく含まない形dp/dt=fになる。いいかえれば、この形に書き換えた運動の第二法則は、質点の種類に無関係な形になる。この場合の座標と運動量という力学変数は、運動の法則を、質点の属性、すなわち質量に無関係な形にする特別な1組の力学変数である。ところで、解析力学の理論は一般的なものであるが、もしこの理論のなかに、個々の力学系の属性(たとえば質点の質量など)が表れていると、理論の一般性を失うことになる。以上のように、質点の座標や運動量に相当するものを、解析力学の対象とする力学系に対して一般的に定義することができる。これを一般化座標qrおよび一般化運動量prという。これらの力学変数は複数組あるのが普通であって、添え字をつけてこれらを区別する。
座標xと運動量pとは、すでに述べたように特別の関係にある力学変数であるが、一般化座標qrと一般化運動量prとの間の関係も同様であって、これを互いに正準共役(きょうやく)な力学変数、または正準変数という。
[田中 一]
ラグランジュ運動方程式とハミルトン運動方程式
どの力学系にも、力学系の全内容を示す物理量がある。解析力学ではこの種の物理量から一般的な運動方程式を導いている。力学系を実際に解く場合には、この種の物理量を力学系ごとに定まる関数で表し、それから導かれる解析力学の運動方程式を解けばよい。
この種の関数にはラグランジュ関数Lとハミルトン関数Hとがある。ラグランジュ関数Lは、力学系の運動エネルギーTからポテンシャルエネルギーVを減じたT-Vを、一般化座標qrとその時間変化dqr/dtの関数として与えたものである。dqr/dtのことを簡単に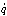 rと書く。この場合の運動方程式をラグランジュの運動方程式といい、一般化座標の微分方程式となっている。
rと書く。この場合の運動方程式をラグランジュの運動方程式といい、一般化座標の微分方程式となっている。
これに対して、力学系のエネルギーT+Vを一般化座標qrと一般化運動量prで表現したものを、ハミルトン関数Hという。この場合の運動方程式はqrとprの連立微分方程式の形をしており、ハミルトンの運動方程式という。正準共役な力学変数qrとprとの間の特別な関係およびqrとprの関数である任意の物理量(qrとprを含む)の時間変化は、いずれも後述のポアソンの括弧(かっこ)式という量を用いて書き表すことができる。また、このときの関係式は、ポアソンの括弧式の定義を変えただけで量子力学にもそのまま成り立つ。このことは、すでに述べたように、解析力学では粒子とその集まりの系にも、また波動としての光にも同一の形式の運動方程式が成り立つこと、すなわち粒子と光の双方に共通する普遍的な法則が存在することを示していて興味深い。次にラグランジュの運動方程式とハミルトンの運動方程式を示しておく。
(1)ラグランジュの運動方程式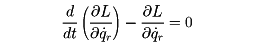
(2)ハミルトンの運動方程式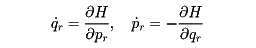
なお、FとGとのポアソンの括弧式は、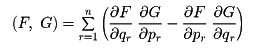
正準共役な関係は、次の1組の式で
(qr, pr)=1, (qr, ps)=0
ただしr≠s
(qr, qs)=0, (pr, ps)=0
r, sは任意
また物理量Fの時間変化は(dF/dt)=(F, H)で表すことができる。
[田中 一]
『小出昭一郎著『解析力学』(1983・岩波書店)』▽『並木美喜雄著『解析力学』(1991・丸善)』▽『山本義隆・中村孔一著『解析力学1・2』(1998・朝倉書店)』▽『久保謙一著『解析力学』(2001・裳華房)』▽『高橋康・柏太郎著『量子場を学ぶための場の解析力学入門』増補第2版(2005・講談社)』
ブリタニカ国際大百科事典 小項目事典 「解析力学」の意味・わかりやすい解説
解析力学
かいせきりきがく
analytical dynamics
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「解析力学」の意味・わかりやすい解説
解析力学【かいせきりきがく】
出典 株式会社平凡社百科事典マイペディアについて 情報
関連語をあわせて調べる
お知らせ
4/12 日本大百科全書(ニッポニカ)を更新
4/12 デジタル大辞泉を更新
4/12 デジタル大辞泉プラスを更新
3/11 日本大百科全書(ニッポニカ)を更新
2/13 日本大百科全書(ニッポニカ)を更新
