束（数学）（読み）そく（英語表記）lattice

日本大百科全書(ニッポニカ)

束（数学）
そく
lattice

順序が定義されている集合Lがあって、Lの任意の二元a、bからなる集合｛a,b｝がつねに上限と下限をもつときLは束であるという。ここに、たとえばuが｛a,b｝の上限であるとは、uがLの元であってu≧a,u≧bが成り立ち、しかもx≧a,x≧bなるLの元xに対してはu≦xが成り立つことをいう。別のことばでいえば上限とは最小上界である。同様に、下限とは最大下界である。

［足立恒雄］

束の例

（1）一つの集合Mをとり、Mの部分集合の全体をLとする。Lの元a、bに対してa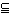b（aはbの部分集合）のときa≦bと定義する。この順序の定義によりLは束をなす。a、bをLの任意の二元とするとき、｛a,b｝の上限はa∪b（a、bの和集合）であり、下限はa∩b（a、bの共通部分）である。

（2）Nを自然数全体の集合とする。自然数aが自然数bを割り切るとき、a≦bと定義すると、Nはこの順序の定義により束をなす。任意の二つの自然数a、bに対して、｛a,b｝の上限はa、bの最小公倍数であり、下限は最大公約数である。

　束という概念は非常に幅の広い基本的な概念であって、いろいろな分野に登場する。

［足立恒雄］

束の基本性質

束Lにおいて｛a,b｝の上限を（集合の場合の類似で）a∪bで表し、下限をa∩bと表すことにすると、次の性質が成り立つ。

(1)べき等律　a∪a＝a, a∩a＝a
(2)交換律 　a∪b＝b∪a,
　　　　　　　a∩b＝b∩a
(3)結合律　(a∪b)∪c＝a∪(b∪c),
　　　 　　　 (a∩b)∩c＝a∩(b∩c)
(4)吸収律　(a∪b)∩a＝a,
　　　　　　　(a∩b)∪a＝a
　逆に、ある集合Lにおいて二つの演算∪、∩が定義されており、上記の交換律、結合律、吸収律の三法則が成り立てば、Lはa∪b＝bのときa≦bと定義することによって束となる。a∪b＝bはa∩b＝aと自然に同値となる。この束の定義からわかるように、Lにおけるある定理において∪と∩とを入れ換えれば、もう一つのLの定理が得られることは明らかで、この事実を双対性(そうついせい)という。射影幾何学の双対性は束の双対性として説明される。応用目的に応じて、種々の束がある。なかでも、完備束、ブール束（ブール代数）、モジュラー束など固有の深い研究がなされている。

［足立恒雄］

[参照項目] | 双対性

出典　小学館　日本大百科全書(ニッポニカ)