日本大百科全書(ニッポニカ) 「数理統計」の意味・わかりやすい解説
数理統計
すうりとうけい
数理統計は大略二つの部分に分けられる。第一は資料の整理ともいうべき部分で、観察や測定などの結果として多数の数値が得られたとき、これらを分析整理して全体的な性質を数量的に把握しようとするものである。第二の部分は偶然的変量に対して統計的な推測を行うことを目標としている。統計的推測の意味は確率のことばを用いて初めて明確になるものである。
以下、(一)では、前記の第一の部分のうち、度数分布表、平均値、標準偏差、相関表、相関係数について説明する。前記の第二の部分では仮説検定と推定が重要な内容であるが、これらについてはそれぞれの項目があるので、それらを見られたい。(二)では、検定、推定の基本である母集団と標本について述べる。次に(三)では、1971年(昭和46)に赤池弘次博士によって提唱されたAIC(Akaike Information Criterion)理論に簡単に触れておく。この新理論の有用性は各国でも認められ注目されている。
[古屋 茂]
(一)資料の整理
(1)度数分布表・ヒストグラム
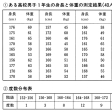
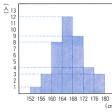
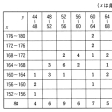
ある高校の男子1年生40人について身長と体重を測定しての①を得た。この表のままでは、身長、体重に関する全体的性質がとらえにくい。初めに身長だけに着目して、次のように身長を区間に分けて、その区間に入る生徒数を数えるとの②ができる。の②で152~156と書いたのは、身長が152センチメートル以上156センチメートル未満という意味で、以下同様である。この区間を階級、階級に属する資料の個数(ここでは生徒数)を度数、各階級に度数を対応させた表を度数分布表という。一つの階級の両端の相加平均をその階級の階級値という。このように度数分布表にすると身長の分布状況が見やすくなる。さらにまた、度数分布表の階級を定める両端の値を横軸上にとり、それぞれの階級を表す区間の上側に、それを底辺とし、対応する度数を高さとする長方形をつくる。この図をヒストグラムという。このようにすると身長の分布のようすがよりいっそう見やすくなる。
[古屋 茂]
(2)平均値・標準偏差・分散
変量x(たとえば(1)であげた例の身長)のn個の観測値をx1、x2、……、xnとするとき、これらn個の相加平均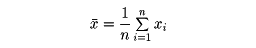
をxの平均値という。階級に分けた度数分布表から平均値を計算するには次のようにする。変量xの階級値がx1、x2、……、xkで、その度数がそれぞれf1、f2、……、fkであるとすると、平均値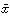 は
は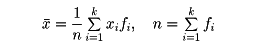
で与えられる。なお、初めの資料そのものから直接に計算した平均値と、初めの資料から度数分布表をつくり、その度数分布表から前記のようにして計算した平均値とは正確には一致しないのが普通である。それは、度数分布表をつくったとき各階級に属する観測値をその階級値で置き換えるからである。
次に標準偏差に移る。変量xのn個の観測値x1、x2、……、xnに対して、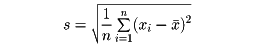
をxの標準偏差といい、s2を分散という。xの標準偏差はn個の観測値x1、x2、……、xnの値の広がりの度合いを表している。度数分布表から標準偏差を求めるには、変数xの階級値がx1、x2、……、xkでその度数がそれぞれf1、f2、……、fkであるとき、標準偏差sは次式で与えられる。
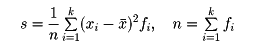
s2を分散という。
[古屋 茂]
(3)相関表・相関係数
(1)でみたように、変量xに関する資料を度数分布表にすると全体のようすがわかりやすくなった。二つの変量x、yに関する資料の場合にも組分けをして表の形にすると、二つの量xとyの間の関係が見やすいものとなる。例として(1)であげた身長・体重の資料を基にして、xを身長、yを体重として、両方を区間に分けて、xがある区間、yがある区間に入る生徒数を数えてをつくる。この表を相関表という。なお空欄のところは0である。相関表をつくると、二つの量xとyとの間の関係がわかりやすくなる。二つの変量xとyとの関連の度合いを測る一つの尺度として相関係数がある。二つの変量xとyについてのn個の観測値
(x1, y1), (x2, y2),……, (xn, yn)
が得られたとする。このとき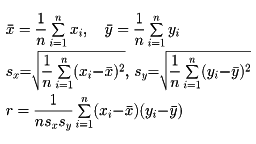
を、x、yの相関係数という。相関係数rに対して次の関係が成り立つ。
-1≦r≦1
rが正数であれば、xの増減はyの増減とほぼ一致する傾向にあり、rが負数であれば、xの増減はyの増減と逆になる傾向がある。またrが1に近ければ、xとyとの間にはほぼy=αx+β(α>0)なる関係があり、rが-1に近ければ、ほぼy=αx+β(α<0)なる関係がある。次に、相関表から相関係数を求めるには次のようにすればよい。xの階級値をx1、x2、……、xk、yの階級値をy1、y2、……、ykとして、xが階級値xiの階級に属し、yが階級値yjの階級に属している資料の個数をfijと置く。このとき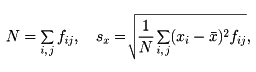
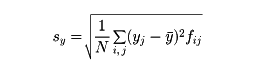
として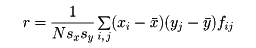
である。例として前記の身長・体重の相関表から相関係数rを求めるとr=0.61である。
[古屋 茂]
(二)母集団と標本
統計調査には全数調査と標本調査とがある。問題としている集団の全部のものについて調査するのが全数調査である。集団の一部を選び出して調査し、その結果から集団全部の状況を推測するのが標本調査である。たとえば、工場の製品の良否を調べるのに検査のため製品を破壊しなければならないことがある。このような場合には全数調査は不可能であって標本調査によらなければならない。また全数調査が可能であっても、そのため多大な費用がかかるとき、または長時間が必要なときなど標本調査が利用されることも多い。標本調査の場合に、もとの集団から選び出された一部のものを標本、標本を構成する要素の個数を標本の大きさという。標本に対してもとの集団を母集団といい、母集団を構成する要素の個数を母集団の大きさという。標本調査においては、母集団から抜き出した標本の性質を調べて母集団の性質を推測するのが目的である。したがって母集団の性質がよく反映されるように標本を選び出さなければならない。そのためには母集団のどの要素も同じ確率で抜き出されるようにする。このように抜き出す方法を無作為抽出または任意抽出という。またこうして得られた標本を無作為標本または任意標本という。
母集団は調査対象に関する資料の集団であるが、その資料は、たとえば身長のように、ある変量xの数値である場合が多い。そこでここでは母集団の資料は変量xの数値と考えることにする。この数値を全部並べたものをx1、x2、……、xNとする。ここでNは母集団の大きさである。このとき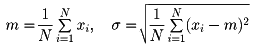
として、mを母平均、σを母標準偏差、σ2を母分散という。また大きさNの母集団において、変量xの異なる値をx1、x2、……、xMで表し、xiという値をとる要素の個数をfiで表すと
N=f1+f2+……+fM
である。この母集団から1個の要素を無作為抽出すると、その要素のxの値がxiである確率はfi/Nである。したがって、母集団から1個の要素を無作為抽出し、その要素のxの値を確率変数Xと考えると、Xの確率分布は、各xiに確率piを対応させたものである。この確率分布を母集団の分布という。この確率変数Xの平均値、標準偏差、分散がそれぞれ母平均、母標準偏差、母分散と一致している。
母集団のなかから大きさ1の標本を無作為抽出することを何回か続けるとき、抽出した標本を毎回もとに戻す場合と、毎回もとに戻さない場合を区別して考える必要がある。前者を復原抽出、後者を非復原抽出という。母集団から第i回目に抽出した要素のxの値は確率変数であるからこの確率変数をXiで表すと、復原抽出の場合にはX1、X2、……、Xnは独立であり、非復原抽出の場合は独立ではない。大きさNの母集団を考え、母平均m、母標準偏差σとする。この母集団から大きさnの無作為標本を取り出し、その標本の相加平均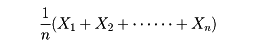
を標本平均といい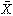 で表す。復原抽出の場合には、
で表す。復原抽出の場合には、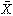 の平均値はm、
の平均値はm、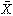 の標準偏差はσ/
の標準偏差はσ/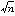 である。非復原抽出の場合には、
である。非復原抽出の場合には、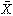 の平均値はm、
の平均値はm、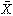 の標準偏差は
の標準偏差は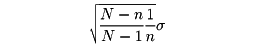
である。母平均mの値は普通は未知である。標本平均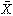 はmの値を推定するのに用いられる。
はmの値を推定するのに用いられる。
[古屋 茂]
(三)情報量統計学
赤池弘次は、実際の統計的データの処理に関する多年の経験に基づいて、数理統計においてきわめて重要な新理論を創始した。すなわち、従来は推定や仮説検定として取り扱われてきた数理統計の諸問題を、モデルの構成と情報量の評価という一貫した視点から見直したのである。統計的モデルの適切さを測る尺度として情報量規準(AIC)は次のように定義される。
AIC=(-2)loge(最大尤度)
+2(パラメーター数)
AICはその値が小さいほうがよいモデルとみなされる。ここで最大尤度(ゆうど)というのは、問題とする確率密度を
f(x,θ)(θ=(θ1,……,θp)
はパラメーター)
とするとき、データx1、……、xNから尤度f(x1,θ)……f(xn,θ)を最大にするようにθを定めた(最尤法)ときの尤度である。また、パラメーター数というのは、モデル内で自由に変化させることのできるパラメーターの個数である。
[古屋 茂]
『河田敬義・丸山文行著『数理統計』新版(1966・裳華房)』▽『『数理科学153号 特集「情報量基準」』(1976・サイエンス社)』▽『坂本慶行・石黒真木夫・北川源四郎著『情報科学講座 情報量統計学』(1983・共立出版)』▽『西平重喜著『新数学シリーズ8 統計調査法』改訂版(1985・培風館)』