改訂新版 世界大百科事典 「解析的整数論」の意味・わかりやすい解説
解析的整数論 (かいせきてきせいすうろん)
analytic number theory
解析的な手法をおもな研究の方法とする整数論の一分野。解析学と整数論は一見あまり関係がないように思われる。しかし整数論においても,種々の関数が自然に現れてくる。例えば,L.オイラーは次のような関数を考えた。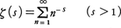 これは,後にG.F.リーマンがこの関数について深い研究をしたので,リーマンのゼータ関数Riemann zeta functionと呼ばれている。オイラーはζ(s)について,いくつかの重要な発見をしたが,その一つとして次の無限積によるζ(s)の表示式を見いだした。
これは,後にG.F.リーマンがこの関数について深い研究をしたので,リーマンのゼータ関数Riemann zeta functionと呼ばれている。オイラーはζ(s)について,いくつかの重要な発見をしたが,その一つとして次の無限積によるζ(s)の表示式を見いだした。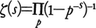 右辺のpは素数全体を動く。右辺の表示はオイラー積Euler productと呼ばれるが,この等式は2以上の自然数が素数の積に一意的に分解できるという定理と同値である。また整数論のある種の問題においては,解析学が重要な方法となることがある。P.G.L.ディリクレは次の算術級数の素数定理と呼ばれる定理を証明した。aとmが互いに素な自然数であるとし,初項がa,公差がmである等差数列a,a+m,a+2m,……を考える。この数列の中に素数が無限に現れるであろうか。このことは,A.M.ルジャンドルによって予想されていたが,ディリクレは1837年にこの定理の証明を与えた。ディリクレは,ζ(s)に指標χを付けたL関数と呼ばれる関数,
右辺のpは素数全体を動く。右辺の表示はオイラー積Euler productと呼ばれるが,この等式は2以上の自然数が素数の積に一意的に分解できるという定理と同値である。また整数論のある種の問題においては,解析学が重要な方法となることがある。P.G.L.ディリクレは次の算術級数の素数定理と呼ばれる定理を証明した。aとmが互いに素な自然数であるとし,初項がa,公差がmである等差数列a,a+m,a+2m,……を考える。この数列の中に素数が無限に現れるであろうか。このことは,A.M.ルジャンドルによって予想されていたが,ディリクレは1837年にこの定理の証明を与えた。ディリクレは,ζ(s)に指標χを付けたL関数と呼ばれる関数,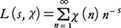 を考え,この関数の1での値L(1,χ)が0でないことから上の定理を導いた。このようにディリクレは解析学が整数論において重要な方法となり得ることを示した。これが解析的整数論の出発点となった。リーマンは当時建設されつつあった一変数解析関数の理論を応用して,さらに大きな一歩を進めた。オイラーもディリクレも変数を実数として考えていたが,リーマンはζ(s)を複素数変数の関数として考察することが本質的であることを洞察し,ζ(s)の性質,とくにその零点のようすが素数の分布と深く関係していることを示し,ζ(s)の零点について重要な予想(リーマン予想)を提出した。J.S.アダマールとC.ド・ラ・バレ・プッサンはリーマンの考えを基にして,C.F.ガウスが予想した素数定理を証明した。その後も,素数分布や,ゼータ関数,L関数の詳しい性質の研究は,解析的整数の中心的な問題として,E.ランダウ,G.H.ハーディー,J.E.リトルウッドなどの人々によって続けられた。またゴルドバッハの予想,ウェアリングの問題なども解析的手法で取り扱われるようになり,加法的整数論additive number theoryと呼ばれる分野ができてきた。
を考え,この関数の1での値L(1,χ)が0でないことから上の定理を導いた。このようにディリクレは解析学が整数論において重要な方法となり得ることを示した。これが解析的整数論の出発点となった。リーマンは当時建設されつつあった一変数解析関数の理論を応用して,さらに大きな一歩を進めた。オイラーもディリクレも変数を実数として考えていたが,リーマンはζ(s)を複素数変数の関数として考察することが本質的であることを洞察し,ζ(s)の性質,とくにその零点のようすが素数の分布と深く関係していることを示し,ζ(s)の零点について重要な予想(リーマン予想)を提出した。J.S.アダマールとC.ド・ラ・バレ・プッサンはリーマンの考えを基にして,C.F.ガウスが予想した素数定理を証明した。その後も,素数分布や,ゼータ関数,L関数の詳しい性質の研究は,解析的整数の中心的な問題として,E.ランダウ,G.H.ハーディー,J.E.リトルウッドなどの人々によって続けられた。またゴルドバッハの予想,ウェアリングの問題なども解析的手法で取り扱われるようになり,加法的整数論additive number theoryと呼ばれる分野ができてきた。
次に解析的整数論における話題をいくつか述べる。
素数分布distribution of prime number
実数xに対して,π(x)でx以下の素数の個数を表すことにする。素数の分布の研究において,xが増大するときに,π(x)がどのように大きくなっていくかを記述することは基本的な問題である。リーマンはζ(s)とπ(x)の間の深い関係を見いだし,π(x)のようすを調べるのにζ(s)を用いることを考えた。リーマンは,ζ(s)を複素変数sの関数と考えると,全複素平面に有理型関数として拡張できることを示し,さらに関数等式,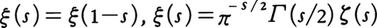 が成り立つことを示した。ここでΓ(s)はガンマ関数である。これからs=-2,-4,……,-2n,……でζ(s)が0になることがわかるが,リーマンはそれ以外のζ(s)の零点はすべてs=1/2+it(tは実数)という形であろうと予想した。これが有名なリーマン予想であるが,今日でも解決されていない。リーマンの予想を仮定すると素数定理より詳しい式,
が成り立つことを示した。ここでΓ(s)はガンマ関数である。これからs=-2,-4,……,-2n,……でζ(s)が0になることがわかるが,リーマンはそれ以外のζ(s)の零点はすべてs=1/2+it(tは実数)という形であろうと予想した。これが有名なリーマン予想であるが,今日でも解決されていない。リーマンの予想を仮定すると素数定理より詳しい式,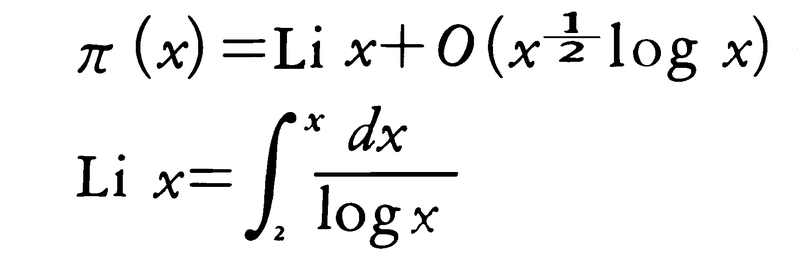
が示されることがわかっているが,現在までに得られている結果はこれにはほど遠い。
加法的整数論
1770年ころ,ウェアリングEdward Waring(1734-98)は,kが自然数であるとき,ある自然数sがあって,任意の自然数Nは,
N=a1k+a2k+……+ask
と,0または自然数a1,……,asのk冪(べき)の和として表されることを予想した。これは,ウェアリングの問題と呼ばれ,D.ヒルベルトによって解決された。ハーディーとリトルウッドはこの証明に別の方法を用いることを考えたが,それによれば,kが与えられたとき,sをどの程度大きくすればよいかということもわかり,またN=ak1+……+ak sとなるa1,……,asの組の個数rs(N)の漸近式も得られる。その方法は,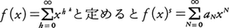 の係数anがrs(N)に等しいことから,rs(N)をf(x)sの積分で表し,sを適当に大きくするとその積分が実際に正になることを示すのである。そのときの積分の大きさを評価する方法は円周法と呼ばれ,重要な方法の一つとなっている。この問題は,主としてsの大きさについて,I.M.ビノグラドフらによりさらに詳しい研究が続けられている。
の係数anがrs(N)に等しいことから,rs(N)をf(x)sの積分で表し,sを適当に大きくするとその積分が実際に正になることを示すのである。そのときの積分の大きさを評価する方法は円周法と呼ばれ,重要な方法の一つとなっている。この問題は,主としてsの大きさについて,I.M.ビノグラドフらによりさらに詳しい研究が続けられている。
この分野の問題としては,ほかにゴルドバッハの予想や,分割数p(n)(自然数nを自然数の和として表すときの表し方の個数,例えば,3=1+1+1=1+2。だからp(3)=3)の大きさの評価の問題などがある。例えば,ハーディーとS.ラマヌジャンにより,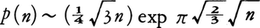 という結果が知られている。
という結果が知られている。
執筆者:齋藤 裕
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「解析的整数論」の意味・わかりやすい解説
解析的整数論
かいせきてきせいすうろん
微分積分学をはじめとする解析的方法を整数論に適用する学問をいう。その創始はドイツの数学者ディリクレによる。たとえば、すべての素数の逆数の和を考えてみる。
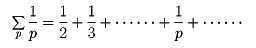
ここにpはすべての素数を動く変数である。実はこの級数は発散する。かりに素数が有限個しかないとすれば、その逆数和は有限の値となるのだから、この級数の発散は素数が無限に存在することを意味する。11と13、17と19のように差が2の素数の組を双子素数(ふたごそすう)という。qでもって双子素数を動く変数を表すことにすると、級数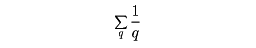
は収束する。これが発散すれば双子素数は無数にあることが結論されるが、それはいえない。ただ、ある意味で双子素数はかなり数が少ないことがいえる。
このように級数が整数論に応用されて多大な成果をもたらす。なかでもディリクレの算術級数定理は有名で、また重要でもある。aを初項、dを公差とする等差級数(算術級数)を考える。
an=a+(n-1)d
aとdとが互いに素であれば、anの形をした素数の逆数の和はつねに発散する。すなわちanのなかには無数に素数が存在する。これをディリクレの算術級数定理という。たとえばdを10としaを1とすると、11、31、41、61、……のように1桁(けた)目が1である素数が無数に存在する。
[足立恒雄]
素数定理
関数論の応用例としてもっとも典型的であり、しかも解析的整数論においてもっとも基本的なのが、素数定理である。正の数xを超えない素数の個数をπ(x)と表すことにする。たとえば
π(10)=4, π(100)=25, π(107)=164579
である。素数の分布に関するもっとも荒っぽいのはπ(2x)-π(x)≧1がx≧2のとき成り立つことを主張する定理であろう。すなわち、xと2xの間にかならず素数が存在する。この程度の定理でも証明はそうやさしくはない。ガウスは15歳のころ、xが大きくなると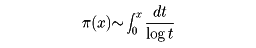
すなわち、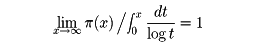
であることを知ったと述べている。
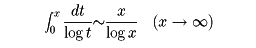
だから、素数定理は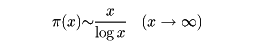
とも述べられる。証明は1896年に至ってアダマールとド・ラ・バレ・プサンCh. de la Vallée-Poussinによって与えられた。そのほか、リーマンのゼータ関数など、解析的整数論固有の問題があって、現在も研究されている。
[足立恒雄]
ブリタニカ国際大百科事典 小項目事典 「解析的整数論」の意味・わかりやすい解説
解析的整数論
かいせきてきせいすうろん
analytic number theory
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内の解析的整数論の言及
【整数論】より
…ディリクレはこの解析学を用いる方法で算術級数の定理の証明を与えた。ディリクレの方法を発展させていく中から解析的整数論ができてきた。ディリクレに引き続いて現れたクンマーは,フェルマーの大定理の研究から出発して,xn-1=0の根で生成される円分体を詳しく研究した。…
※「解析的整数論」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
今日のキーワード
焦土作戦
敵対的買収に対する防衛策のひとつ。買収対象となった企業が、重要な資産や事業部門を手放し、買収者にとっての成果を事前に減じ、魅力を失わせる方法である。侵入してきた外敵に武器や食料を与えないように、事前に...
お知らせ
4/12 日本大百科全書(ニッポニカ)を更新
4/12 デジタル大辞泉を更新
4/12 デジタル大辞泉プラスを更新
3/11 日本大百科全書(ニッポニカ)を更新
2/13 日本大百科全書(ニッポニカ)を更新
