精選版 日本国語大辞典 「距離」の意味・読み・例文・類語
出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報
出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報
数学では、以下のようないろいろな場合に分けて距離を定義する。(1)2点間の距離 2点A、Bを結ぶ線のなかでもっとも短いのは線分ABで、その長さが2点A、B間の距離である。(2)点と直線の距離 点Aと直線l上の任意の点とを結ぶ線のなかでもっとも短いのはAからlへ下ろした垂線AHで、その長さをAとlの距離という。(3)点と平面の距離 点Aと平面α上の任意の点とを結ぶ線のなかでもっとも短いのは、Aからαへ下ろした垂線AHで、その長さをAとαの距離という。(4)平行2直線の距離 平行な2直線l、mについて、両方に垂直な直線がl、mと交わる点をA、Bとすると、線分ABの長さは共通の垂線をどこにとっても一定である。この長さを平行2直線l、mの距離という。(5)平行2平面の距離 平行な2平面α、βについて、両方に垂直な直線がα、βと交わる点をA、Bとするとき、線分ABの長さを2平面α、βの距離という。(6)ねじれの位置にある2直線の距離 2直線をp、qとし、p上に任意の点P、q上に任意の点Qをとるとき、P、Qを結ぶ線のなかでもっとも短いのは、p、qの両方に垂直な線分PQで、これを2直線p、qの距離という。このときのp、qの両方に直交する直線PQはただ一つあって、p、qの共通垂線という。
[栗田 稔]
(1)平面上で、2点A、Bの直交座標が(a1, a2), (b1, b2)のとき、距離は、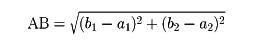
空間で、2点A、Bの直交座標が(a1, a2, a3), (b1, b2, b3)のとき、距離は、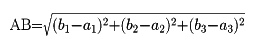
(2)直交座標で、点Pの座標が(x1, y1)、直線pの方程式がax+by+c=0のとき、Pとpの距離PHは、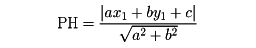
直交座標で、点Pの座標が(x1, y1, z1)、平面αの方程式がax+by+cz+d=0のとき、Pとαの距離PHは、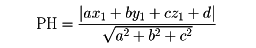
である。
[栗田 稔]
三次元空間内の2点P,Qに対し,PをQに結ぶ線分PQの長さをPとQの距離という。直交座標によりP,Qをそれぞれ(x1,y1,z1),(x2,y2,z2)で表すとき,PとQの距離は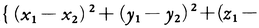
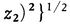 で与えられる。空間内の二つの図形α,βに対し,αの点Pとβの点Qの距離の,P,Qをいろいろに動かしたときの下限をαとβの距離という。αが直線または平面のとき,α上にない1点Pとαの距離はPからαに下ろした垂線の長さに等しい。α,βがともに直線か平面で,αとβが交わらないとき,αとβの距離はαとβの共通垂線の長さに等しい。点(x0,y0,z0)とax+by+cz+d=0(a,b,c,dは定数)で表される平面の距離は
で与えられる。空間内の二つの図形α,βに対し,αの点Pとβの点Qの距離の,P,Qをいろいろに動かしたときの下限をαとβの距離という。αが直線または平面のとき,α上にない1点Pとαの距離はPからαに下ろした垂線の長さに等しい。α,βがともに直線か平面で,αとβが交わらないとき,αとβの距離はαとβの共通垂線の長さに等しい。点(x0,y0,z0)とax+by+cz+d=0(a,b,c,dは定数)で表される平面の距離は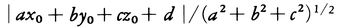 で ある。曲面S上の2点P,Qに対し,PをQに結ぶS上の曲線の長さの,曲線をいろいろにとったときの下限をPとQのS上での距離という。Sが球面のときは,これはP,Qを通る大円上の劣弧
で ある。曲面S上の2点P,Qに対し,PをQに結ぶS上の曲線の長さの,曲線をいろいろにとったときの下限をPとQのS上での距離という。Sが球面のときは,これはP,Qを通る大円上の劣弧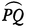 の長さとなる。
の長さとなる。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
出典 平凡社「普及版 字通」普及版 字通について 情報
…平面上の2点P,Qの距離をd(P,Q)で表したとき,次の3条件が成り立つ。(1)d(P,Q)≧0でかつP=Qのときに限ってd(P,Q)=0,(2)d(P,Q)=d(Q,P),(3)d(P,R)≦d(P,Q)+d(Q,R)。…
…この立場の集合は単なる点の集りとしての集合ではない。ユークリッド空間を距離空間と考えて,その意味での位相や,長さ,面積,体積などを考慮に入れて考えたものである。したがって,多くの事柄が位相空間論へと一般化される。…
※「距離」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
血液中の脂質(トリグリセリド、コレステロールなど)濃度が基準値の範囲内にない状態(脂質異常症)に対し用いられる薬剤。スタチン(HMG-CoA還元酵素阻害薬)、PCSK9阻害薬、MTP阻害薬、レジン(陰...
4/12 日本大百科全書(ニッポニカ)を更新
4/12 デジタル大辞泉を更新
4/12 デジタル大辞泉プラスを更新
3/11 日本大百科全書(ニッポニカ)を更新
2/13 日本大百科全書(ニッポニカ)を更新