日本大百科全書(ニッポニカ) 「弾性」の意味・わかりやすい解説
弾性
だんせい
ばねやゴムを伸ばして放すと長さは元に戻る。このように物体に力を加えると変形するが、力を除くと元の形に戻るとき、この物体は弾性をもつという。固体だけでなく、注射器の先をふさいでピストンを押して離すと元に戻ることからわかるように、液体や気体も圧縮に対して弾性を示す。弾性体に加えた力があまり大きくない範囲では、力と変形とは比例する（これを線形弾性という。フックの法則が成り立つ）。この力と変形の比をその物体の弾性スティフネス、その逆数を弾性コンプライアンスという。
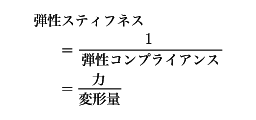
弾性スティフネスは、その物体の性質（弾性率）だけでなく、物体の寸法によって変わる。たとえば物体を一方向に伸ばすとき、張力は力Fを物体の断面積Aで割った量であり、伸びのひずみは伸び量Δlを元の長さlで割った量であるから、
弾性スティフネス＝F/Δl＝(ヤング率)×(A/l)
となる。ここでヤング率は弾性率（応力とひずみの比）の一種で、物質固有の性質である。つるまきばねの場合、伸びの弾性スティフネスは
πr4G/2lR2
である。ここでlは針金の全長、rは針金の半径、Rはつるまきばねの半径、Gは針金のずり弾性率である。
［和田八三久・西 敏夫］
弾性エネルギー
ばねを外力によって伸ばすときは、外力がばねに仕事をする。逆にこのばねが元に戻るとき、ばねにつながれたものに仕事をすることができる。すなわち、ばねを伸ばすときに外からした仕事は、伸びたばねの中に位置エネルギーとして蓄えられている。このエネルギーを弾性エネルギーという。弾性体を伸ばす場合でいうと、弾性エネルギーUは、Sを弾性スティフネスとして、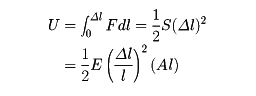
となる。Eはヤング率である。(Al)は弾性体の体積であるから、
(1/2)E(Δl/l)2
すなわち一般に
(1/2)×(弾性率)×(ひずみ)2
が単位体積当りの弾性エネルギーである。これを弾性エネルギー密度という。
［和田八三久・西 敏夫］
弾性波
ばねにおもりをつるして伸ばして放すと、おもりは元の位置に戻ったとき、なお上向きの速度をもっているから、さらにばねを縮めて上に昇り、以下上下の振動を繰り返す。これはおもりが質量（慣性）をもっているために、おもりの運動エネルギーとばねの弾性エネルギーとの間でエネルギーのやりとりが繰り返されるからである。これを弾性振動という。
一般に物体は弾性とともに密度をもっているので、一度、物体のどこかにひずみを与えると、このひずみは物体中を弾性振動の波として伝わっていく。これを弾性波（あるいは広い意味での音波）という。等方的な弾性体では一般に二つの独立な弾性率（体積弾性率とずり弾性率）があることに対応して、2種類の弾性波があり、一方は縦波(たてなみ)、他方は横波(よこなみ)である。両者の伝搬速度は、体積弾性率K、ずり弾性率Gを用いて、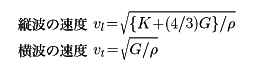
となる。ρは密度である。
液体や気体ではG＝0であるから横波は存在せず、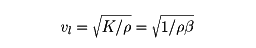
となる。βは圧縮率である。この縦波を圧縮波ともいう。通常の場合、縦波における体積変化は断熱的におこるので、これらの式のKやβは断熱体積弾性率や断熱圧縮率である。
耳に聞こえる音は、空気中を伝わる弾性波（圧縮波）であり、地震の波も地殻中を伝わる弾性波である。物体の内部を伝わる弾性波のほかに、表面を伝わる表面波、細い棒や板の中を伝わる弾性波もある。
［和田八三久・西 敏夫］
弾性の限界
外力が大きくなると、弾性の範囲内でも力と変形とは比例しなくなる（非線形弾性）。この限界を比例限界という。さらに外力を大きくすると、破壊してしまう物質もあるが、金属などでは、外力を取り除いても元に戻らない変形を示す。これを塑性変形あるいは塑性流動という。この塑性流動の始まる点を弾性限界という。さらに変形を増大させれば破壊する。この塑性流動や破壊の仕方は、弾性率とは違って、同じ物質でもその材料のつくり方などによって大きく変わる。
［和田八三久・西 敏夫］
物質が弾性をもつ理由
物質が弾性をもつのは、一つには、物質を構成している分子や原子の間に力が働いていて、物体が変形して分子の間隔が変わると、元（エネルギーの低い状態）に戻ろうとするからである。もう一つの理由は、分子が熱運動をしていて、できるだけ無秩序の状態（エントロピーの大きい状態）に戻ろうとするからである。一般の固体や液体の弾性は主として前者により、気体やゴムの弾性は主として後者による。
［和田八三久・西 敏夫］
『野田直剛・谷川義信・須見尚文・辻知章著『基礎弾性力学』（1988・日新出版）』▽『阿部武治・清水茂俊・山田勝稔著『現代機械工学シリーズ4 弾性力学』（1991・朝倉書店）』▽『高橋邦弘著『弾性力学の基礎』（1998・コロナ社）』▽『中原一郎・渋谷寿一・土田栄一郎・笠野英秋・辻知章・井上裕嗣著『弾性学ハンドブック』（2001・朝倉書店）』