精選版 日本国語大辞典 「平方根」の意味・読み・例文・類語
へいほう‐こん ヘイハウ‥【平方根】
出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報
日本大百科全書(ニッポニカ) 「平方根」の意味・わかりやすい解説
平方根
へいほうこん
数aが与えられたとき、二乗(平方)してaとなる数、つまり、x2=aとなる数xをaの平方根という。aが正の数のときは、aの平方根は正の数、負の数それぞれ一つずつあり、その絶対値は等しい。そして、正のほうを、 と書く。
と書く。 は、ルートaと読む。負のほうは、-
は、ルートaと読む。負のほうは、- で表される。したがって、このとき、aの平方根は、±
で表される。したがって、このとき、aの平方根は、± とまとめられることになる。たとえば、2の平方根は、
とまとめられることになる。たとえば、2の平方根は、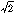 と-
と-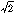 で、±
で、±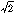 とまとめられる。この場合、記号
とまとめられる。この場合、記号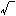 を、根号(または平方根号)という。0の平方根は0だけである。また、負の数の平方根は、実数でなく、虚数である。たとえば-2の平方根は、
を、根号(または平方根号)という。0の平方根は0だけである。また、負の数の平方根は、実数でなく、虚数である。たとえば-2の平方根は、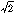 iと-
iと-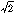 iである(iは虚数単位で、
iである(iは虚数単位で、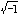 のこと)。
のこと)。
正の整数の平方根について考える。aが平方数、つまり、ある正の整数nの平方の形n2と書かれる数であるときは、 はnに等しい(たとえば
はnに等しい(たとえば 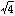 =2)。しかし、aが平方数でないとき、
=2)。しかし、aが平方数でないとき、 は有理数になることはけっしてなく、無理数になる。つまり、有限小数や分数で表されることはなく、循環しない無限小数になる(たとえば
は有理数になることはけっしてなく、無理数になる。つまり、有限小数や分数で表されることはなく、循環しない無限小数になる(たとえば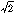 =1.41421356……)。正方形の一辺の長さを1とすれば、対角線の長さは
=1.41421356……)。正方形の一辺の長さを1とすれば、対角線の長さは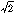 と表されるが、
と表されるが、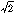 が無理数であることを古代ギリシア人はすでに知っていた。それは、ユークリッドの『原論』にみられる。
が無理数であることを古代ギリシア人はすでに知っていた。それは、ユークリッドの『原論』にみられる。
正の数の平方根について考えているとき、根号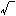 はつねに正の数を表す。これが根号の規約である。すると、a>0のとき
はつねに正の数を表す。これが根号の規約である。すると、a>0のとき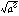 =aであるが、a<0のときa2>0であって、
=aであるが、a<0のときa2>0であって、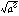 =-aとなる。
=-aとなる。
平方根号の中に平方根が含まれることがある。たとえば、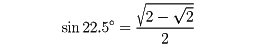
である。このような場合、一般には、二重の平方根号を外すことはできないが、外すことのできる場合がある。a、bが正の整数、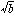 が無理数のとき、
が無理数のとき、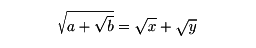
となる正の有理数x、yは、a2-bが有理数の平方の形になるときにだけ存在する。たとえば、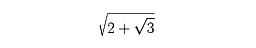
では、22-3=1=12で、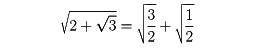
となる。しかし、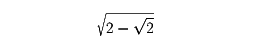
の平方根号は、外すことができない。
[三輪辰郎]
改訂新版 世界大百科事典 「平方根」の意味・わかりやすい解説
平方根 (へいほうこん)
square root
2乗してaとなる数をaの平方根,または2乗根という。
(1)aが正の数のとき,aの平方根は実数で,二つあり,一つは正,もう一つは負で,それらの絶対値は等しい。正の平方根を\(\sqrt{a}\)で表す。
(2)aが0のとき,0の平方根は0である。
(3)aが負の数のとき,aの平方根は二つの純虚数で,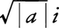 と-\(\sqrt{|a|}\)i(iは虚数単位,i2=-1)である。
と-\(\sqrt{|a|}\)i(iは虚数単位,i2=-1)である。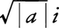 を\(\sqrt{a}\)で表すこともある。
を\(\sqrt{a}\)で表すこともある。
(4)αが0でない複素数のとき,αの平方根は,複素数の範囲で二つあり,その一つがa+bi(a,bは実数)ならば,他の一つは-(a+bi)である。
開平
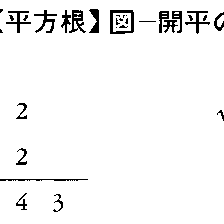
正の数aの平方根を求めることをaを平方に開く,またはaを開平するといい,その計算の方法を開平法という。開平法は,すでにアルキメデスの著書にも見られるが,現在行われている開平法は,16世紀になって見いだされた。この開平法は,平方の公式(x+y)2=x2+2xy+y2を利用する。すなわち,aを正の数とするとき,
(1)2乗すればaより小で,aに近い正の数b1をとる。
(2)\(\sqrt{a}\)-b1=c>0とすれば,a=b12+2b1c+c2である。ここでcはb1に比べて小さいから,c2を無視することにより,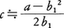 となる。
となる。
(3)そこで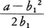 に近く,これより小さい正の数c1をとる。b2=b1+c1とすれば,b2はb1よりさらに\(\sqrt{a}\)に近づく。
に近く,これより小さい正の数c1をとる。b2=b1+c1とすれば,b2はb1よりさらに\(\sqrt{a}\)に近づく。
(4)次に,b1の代りにb2を用い,(2),(3)の操作を行いb3を求める。
(5)以下,(2),(3),(4)を繰り返し,b4,b5,……を求めていけば,n回目にbn=\(\sqrt{a}\)となるか,nが大きくなるにつれ,bnは限りなく\(\sqrt{a}\)に近づく。
例えば,a=552.25のとき,上の(1)~(5)の操作は,図のように図式的に計算できる。
執筆者:西村 純一
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「平方根」の意味・わかりやすい解説
平方根
へいほうこん
square root
z=r(cosθ+i sinθ)(r>0,-π<θ≦π)
とすると,
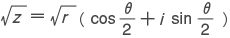 は 2乗すると z になる複素数の一つである。有理数から出発して,その平方根をとる操作および加減乗除(→四則)の操作を繰り返して得られる数は,定規とコンパスで作図することができる数である。たとえば黄金比(→黄金分割)の
は 2乗すると z になる複素数の一つである。有理数から出発して,その平方根をとる操作および加減乗除(→四則)の操作を繰り返して得られる数は,定規とコンパスで作図することができる数である。たとえば黄金比(→黄金分割)の 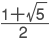 は,定規とコンパスで作図できる。このことから,正五角形は定規とコンパスで作図できることがわかる。
は,定規とコンパスで作図できる。このことから,正五角形は定規とコンパスで作図できることがわかる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「平方根」の意味・わかりやすい解説
出典 株式会社平凡社百科事典マイペディアについて 情報
今日のキーワード
焦土作戦
敵対的買収に対する防衛策のひとつ。買収対象となった企業が、重要な資産や事業部門を手放し、買収者にとっての成果を事前に減じ、魅力を失わせる方法である。侵入してきた外敵に武器や食料を与えないように、事前に...
お知らせ
4/12 日本大百科全書(ニッポニカ)を更新
4/12 デジタル大辞泉を更新
4/12 デジタル大辞泉プラスを更新
3/11 日本大百科全書(ニッポニカ)を更新
2/13 日本大百科全書(ニッポニカ)を更新

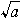 (ルートa)と書く。√は
(ルートa)と書く。√は