精選版 日本国語大辞典 「写像」の意味・読み・例文・類語
しゃ‐ぞう ‥ザウ【写像】
出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報
翻訳|mapping
出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報
2変数の関数f(x,y)は,平面の点(x,y)に,関数の値f(x,y)を,それぞれ定めていると考えられる。この考えを一般にしたものが写像である。つまり,集合Aの各元に,集合Bの元を,ある規則によりそれぞれ定めているとき,この規則をAからBへの写像という。AからBへの写像は,f,φなどの記号を用い,f:A→B,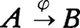 などと表される。
などと表される。
写像f:A→Bにより,Aの元aに,Bの元bが定まっているとき,aにおけるfの値はbであるとか,fはaをbに写すとかいい,f(a)=b,あるいは単にa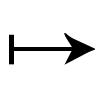 bで表す。このとき,bをfによるaの像という。一般に,Aの部分集合A′に対し,A′の元aのfによる像f(a)の和集合{f(a)|a∈A′}を,fによるA′の像といい,f(A′)で表す。とくにf(A)はfの像と呼ばれる。また,Bの部分集合B′に対し,Aの元でfによる像がB′の中に入るもの全体{a∈A|f(a)∈B′}を,fによるB′の原像,あるいは逆像といい,f⁻1(B′)で表す。
bで表す。このとき,bをfによるaの像という。一般に,Aの部分集合A′に対し,A′の元aのfによる像f(a)の和集合{f(a)|a∈A′}を,fによるA′の像といい,f(A′)で表す。とくにf(A)はfの像と呼ばれる。また,Bの部分集合B′に対し,Aの元でfによる像がB′の中に入るもの全体{a∈A|f(a)∈B′}を,fによるB′の原像,あるいは逆像といい,f⁻1(B′)で表す。
写像f:A→Bにおいて,fの像f(A)がBと一致するとは限らない。そこで,f(A)=Bが成り立つとき,すなわち,Bのどの元bについても,bをfの値とするAの元aが,少なくとも一つ存在するとき,fはAからBへの全射,あるいはAからBの上への写像であるという。また,写像f:A→Bが,Aの任意の異なる2元a,a′に対し,それぞれ異なるfの値を定めているとき,つまり,a≠a′なら,f(a)≠f(a′)であるとき,fはAからBへの単射,あるいはAからBへの1対1の写像であるという。写像f:A→Bが,全射かつ単射であるとき,fはAからBへの全単射であるという。例えば,(1)f(x)=x3-xは実数の全体RからR自身への全射であるが,単射ではない,(2)f(x)=exは,RからRへの単射であるが,全射ではない,(3)f(x)=x5+1は,RからRへの全単射である。
集合Aの部分集合A′の各元aに,a aと定めると,A′からAへの単射写像を得る。この写像を,A′からAへの包含写像という。とくに,A′=Aのとき,Aの恒等写像といい,1a,idaなどと表す。
aと定めると,A′からAへの単射写像を得る。この写像を,A′からAへの包含写像という。とくに,A′=Aのとき,Aの恒等写像といい,1a,idaなどと表す。
集合A,B,Cと,写像f:A→B,g:B→Cを考える。Aの元aに,まずfの値f(a)が,次にf(a)のgの値g(f(a))が定まる。つまり,a f(a)
f(a) g(f(a))により,AからCへの写像を得る。この写像を,fとgの合成写像(または積)といい,g◦fで表す。いま,f,gがともに全射(単射,全単射)ならば,g◦fもまた,全射(単射,全単射)である。また,写像の合成について結合法則が成り立つ。すなわち,集合A,B,C,Dと,写像f:A→B,g:B→C,h:C→Dにおいて,(h◦g)◦f=h◦(g◦f)。
g(f(a))により,AからCへの写像を得る。この写像を,fとgの合成写像(または積)といい,g◦fで表す。いま,f,gがともに全射(単射,全単射)ならば,g◦fもまた,全射(単射,全単射)である。また,写像の合成について結合法則が成り立つ。すなわち,集合A,B,C,Dと,写像f:A→B,g:B→C,h:C→Dにおいて,(h◦g)◦f=h◦(g◦f)。
写像f:A→Bに対し,fの逆対応f⁻1,つまり,Bの元bにbの原像f⁻1(b)を定める対応が,写像になるとは限らない。f⁻1が写像となるための必要十分条件は,fが全単射であることで,そのとき,f⁻1もBからAへの全単射,かつ,f⁻1◦f=1a,f◦f⁻1=1b,(f⁻1)⁻1=fが成り立つ。このf⁻1をfの逆写像という。
執筆者:西村 純一
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
風景と、レンズを通して得られるその像のように、ある対象の点を他の対象の点に写す、または対応させる仕方を写像というが、その考え方はもっと一般化されて、集合、位相空間、群とか体(たい)のような数学的対象においても用いられる。
fが対象AからBへの写像(同様の意味で対応、関数とか射(しゃ)という語が用いられることがある)とは、Aの任意の元xに対して、fによって、Bのただ一つの元が定まるときで、このyのことをxのfによる像といい、x→f(x)とかy=f(x)のように記す。またfがAからBへの写像であることをf:A→BとかA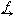 Bのように記す。とくにAの相異なる元に対応するBの元が相異なるときfは一意写像または単射とよばれる。そしてBの任意の元がAの元の像となっているときfは全射とよばれる。特別な場合としてAの元xにそれ自身を対応させる写像1Aは恒等写像とよばれている。恒等写像は全射であると同時に単射でもある。このような写像は全単射とよばれる。
Bのように記す。とくにAの相異なる元に対応するBの元が相異なるときfは一意写像または単射とよばれる。そしてBの任意の元がAの元の像となっているときfは全射とよばれる。特別な場合としてAの元xにそれ自身を対応させる写像1Aは恒等写像とよばれている。恒等写像は全射であると同時に単射でもある。このような写像は全単射とよばれる。
AからBへの写像fが全単射であるとき、Bの任意の元yに対してy=f(x)となるAの元xがただ一つ定まる。yにこのxを対応させる写像をf-1と記して、fの逆写像とよぶ。もちろんAのすべての元についてf-1(f(x))=xであり、Bのすべての元についてf(f-1(y))=yである。
AからBへの写像fについてf(x)が定まっているxの全体、この場合はAをfの定義域、そしてxが定義域を動くときのf(x)の全体の集合をfの値域とよぶ。したがって値域がBに一致する写像が全射である。たとえば、実数から実数への写像として、xにその平方x2を対応させる写像では、定義域は実数の全体、値域はゼロまたは正の実数の全体である。
何個かの写像については合成写像という概念がたいせつである。たとえばfはAからBへの、gはBからCへの写像であるとき、Aの元xに対してfによってBの元f(x)が定まり、さらにgによってCの元g(f(x))が定まる。このようにしてAの元xに対してCの元g(f(x))が定まる。この写像をfとgの合成写像といいg゜fと記する。
さてAからBへの二つの写像fとf′についてAのすべての元xについてf(x)とf′(x)が等しいときfとf′は写像として等しいといい、f=f′と記す。このようにすれば恒等写像についてはf・1A=1B・f=fであり、fが全単射のときは逆写像f-1についてf゜f-1=1Bおよびf-1゜f=1Aが成立する。さらにhをCからDへの写像とすればh゜gはBからDへの写像であるが、二つの異なる仕方でのAからDへの合成写像、つまりh゜(g゜f)と(h゜g)゜fについては、Aの任意の元xに対して両方ともDの元h(g(f(x)))を対応させる写像としてh゜(g゜f)=(h゜g)゜fという結合法則(結合律)が成立する。この点は写像の合成の重要な点である。しかしながらf゜gが定義されていてもg゜fが定義されるとは限らず、両方とも定義されている場合でも一般には等しいとは限らない。つまり一般には交換法則(交換律)は成立しない。
[難波完爾]
出典 株式会社平凡社百科事典マイペディアについて 情報
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
出典 ASCII.jpデジタル用語辞典ASCII.jpデジタル用語辞典について 情報
…
[関数の一般的定義]
前述の関数の概念を一般化して,関数を次のように定義する。 二つの集合X,Yがあって,Xのどの要素xにも,Yの要素yがちょうど一つ対応しているとき,この対応をXからYへの関数,または写像といい,記号fなどを用いて,f:X→Yと書いたり,y=f(x)と書いたりする。前に述べた(イ)~(ニ)の例は,いずれもX,Yが実数の集合の場合であるが,x,yが必ずしも数ではなくても,xを変数と呼び,yはxの関数であるということが多い。…
※「写像」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
血液中の脂質(トリグリセリド、コレステロールなど)濃度が基準値の範囲内にない状態(脂質異常症)に対し用いられる薬剤。スタチン(HMG-CoA還元酵素阻害薬)、PCSK9阻害薬、MTP阻害薬、レジン(陰...
4/12 日本大百科全書(ニッポニカ)を更新
4/12 デジタル大辞泉を更新
4/12 デジタル大辞泉プラスを更新
3/11 日本大百科全書(ニッポニカ)を更新
2/13 日本大百科全書(ニッポニカ)を更新