翻訳｜body
出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報
〈タイ〉
〈テイ〉見かけのようす。「体裁／
［名］
［接尾］名詞・人代名詞などに付いて、そのようなもの、そのようなようすなどの意を表す。「職人―の男」［名］［接尾］助数詞。神仏の像や死体などを数えるのに用いる。「仏像一生物の個体を，一定の構造と機能の統合された完結性と独立性をもつ物体としてみるとき，それを〈体〉という。しかし，体には広狭2種の意味合いがある。広義では生物体とほぼ同義であり，狭義ではヒトを中心とする高等動物の身体をさす。広義で，生物体としての体は，単細胞と多細胞，植物と動物とをとわず，すべての生物個体の物質的実体である。しかし，各種生物の生活環の各段階における個体性，つまり個体のあり方に応じて，体の概念はさまざまである。例えば，細菌や原生動物の体（細胞体）はいろいろな細胞小器官を含むただ1個の細胞であり，雌雄の別はない。これらの生物の増殖様式は種によって多様だが，1個の個体の単純な分裂や出芽による場合と，2個の個体の合体や接合と分裂とを交互に起こす場合とがある。こうした単細胞生物では個体性が必ずしも明確でなく，したがって同一種の生物でも体の概念は一定しない。多細胞生物においても，出芽によって増殖したり，群体をつくる動植物では，複数個体が連結しているうえに非生活物質の殻をもつ場合もあるため，体の概念は不明確である。個体性の明らかな，有性生殖をする高等動植物では，成熟体の体の概念は最も常識的なもので明確であるが，個体発生過程をさかのぼるにつれてその概念は不明りょうになる。また生殖細胞そのものは，独立性をもつように見えても独立生活を営むものではないから，その細胞体は普通の体細胞と同じく，1個の生物体または体とはいえない。このように，生物体としての体はほぼ〈個体〉に対応した多分に便宜的な概念で，その内容は多様であるうえ明確には規定しえない場合が少なくない。
狭義の体は身体，肉体ともいい，一般には頭の先から足やしっぽの先まで外皮に包まれた全体をさすが，ときには四肢を除いた体幹のみをいうこともある。その外皮は〈体〉の内部環境を外部環境から画し，内部環境はホメオスタシスによって恒常性を維持されている。
すべての生物は細胞，組織，器官，器官系という単位から構成されているが，その〈体〉の成立ち，構成（体制）はグループによって著しく異なる。体制上の最も基本的な違いは単細胞生物と多細胞生物であり，多細胞生物については植物と動物が大別される。
植物の中では，根，茎，葉の区別のない菌類，藻類，苔類などが葉状植物と呼ばれるのに対して，蘚類，シダ植物，種子植物は，茎と葉が明りょうに分化しているので茎葉植物と呼ばれ，さらにシダ植物と種子植物は維管束がよく発達しているため併せて維管束植物と呼ばれる。これが植物におけるおおまかな体制上の区分である。
動物においては，原生（単細胞）動物以外のものを後生（多細胞）動物と総称するが，その中で海綿動物だけは明りょうな組織分化がみられない（側生動物）。ついで発生学的に内・外の2胚葉からなる組織をもつもの（刺胞・有櫛（ゆうしつ）動物），さらに内・中・外の3胚葉の分化した原体腔類（扁形・ひも形・線形・輪形動物など）が識別される。さらに進んでは，真の体腔をもつ真体腔類（節足・軟体・環形・有爪（ゆうそう）動物など）に至って基本的な器官系が出そろう。これより複雑なものに腸体腔類（毛顎・棘皮（きよくひ）・原索動物）があり，それからは最も複雑な型である背骨をもつ脊椎動物が区別される。以上が動物におけるおおまかな体制上の区分である。これを進化的にみると，単一の系統にそってではないにせよ，体制の単純なものからより複雑なものが順次に発展してきたということができる。
生物の外形はその立体幾何学的な対称性をもとに類別されることがあり，無軸型（アメーバ），全面相称型（放散虫類），放射相称型（ヒトデ），左右相称型（脊椎動物）などの型が認められている。体の相称性は発生過程における形態形成の様式や，運動性の特徴と密接に結びついたものである。
執筆者：田隅 本生
人体ともいわれるヒトの体の外形は，ほぼ左右対称で，無対の頭と胴（頭から胴の部分を体幹という），1対の上肢と下肢からなる。頭は胴がくびれて細くなった頸（くび）によって支えられる。頭の前面は顔，胴の前面の上方が胸，下方が腹であり，胴の背面は背である。腹と背は会陰部を介して移行している。上肢は胴の外側で胸背移行部の上端から出て，胴に近いほうから順に上腕（二の腕），前腕，手に区分されるが，俗には上肢全体をさして〈手〉ともいう。手の先端には5本の指が分かれる。下肢は胴の下端から出て大腿（ふともも），下腿（すね），足の3部からなるが，上肢と同様，俗には下肢全体をさして〈足〉ともいう。足の先端も5本の指（趾）に分かれる。
体は外皮でおおわれているが，口，鼻孔，肛門，外尿道孔，女性ではさらに腟が外皮を欠く。一方，眼瞼裂と外耳道孔では，外皮は薄くなるが，中断されてはいない。胸部には1対の乳があり，腹の正中線上には，胎生期の母体との交通路が遺存したへそがある。
四肢は芯に骨格をもっているが，頭と胴では，骨格はむしろ体壁の一部をなしており，内部の内臓諸器官を保護している。体を支える軸となる骨格は脊柱で，胴の正中背側部を頸の上端から骨盤まで縦走している。脊柱は椎骨の積重ねでできており，脊椎動物の体幹に共通した体節的構造を示している。脊柱は前後に一定の湾曲をなし，頸部では前湾，胸部で後湾，腰部で前湾する。この湾曲は，出生10ヵ月ごろ，直立歩行する時期から出現する。
脊柱には脊柱管と呼ばれる上下に長い管があり，その上端は頭蓋骨のなかの広い腔所，頭蓋腔と連続し，神経系の中枢をなす中枢神経（脳と脊髄）をこのなかに保護している。
ヒトが直立歩行を行うようになり，脊柱は地表に対して90度回転して垂直方向をとり，発達した重い脳を脊柱の上端にのせるようになった。その結果，頭部は安定した。しかし，直立歩行により脊柱は四足歩行より，より大きな体の重みを受け，腰痛の原因となり，また内臓下垂が起こりやすく，循環系には負担がかかるようになった。体の直立時の重心線は，足関節の中心から5cm前方を通る。一方，直立歩行は上肢（前肢）を歩行から解放し，その運動範囲は著しく拡大し，複雑，かつ繊細，速やかな運動を可能にした。しかし上肢は下肢と比較して細く弱々しく関節も強固ではない。一方，下肢は体の重さを支え，歩行を担当するため太く大きく発達し，関節の結合は堅固であるが，運動の自由度は著しく制約されている。
脊柱の前方には体腔が広がり，その体腔は筋肉性の膜，横隔膜によって胸腔と腹腔に分けられている。これらの体腔には諸器官が内蔵されている。これら諸器官は基本的に無対のものと左右1対のものからなる。無対の器官は，胎生期に正中線上の間膜と呼ばれる体腔を左右に二分する膜内に発生する器官で，血管系，消化器系が含まれる。これに対し，左右対称に発生する器官は，呼吸器と泌尿生殖器である。
男性と女性の体には性差がある。内外の生殖器の違いを一次性徴といい，それ以外で思春期以降に現れるものを二次性徴という。二次性徴としては，外観上次のような性差がみられる。女性の体は一般に男性に比して小柄で，身長で約10cm低く，体重で5～10kg軽い。筋骨の発達は弱く，皮下の脂肪組織がよく発達しているために，女性の体は丸みを帯びている。胴は長く，四肢は短い。乳房は思春期以後発達し，へその位置は男性に比して少し高い。肩幅は狭く，骨盤は幅広く，かつその高さは低い。これに対し男性は，筋骨が発達し，皮下脂肪は少ないために，体表に凹凸が多い。皮膚は厚く，顔面，胸部，下肢などに毛が多い。肩幅は広く，骨盤は狭く，丈が高い。そのために胴は逆三角形を呈し，その横断面は横方向に広がっている。
体の形質は人種によっても異なっている。
（1）コーカソイド（白色人種） 皮膚の色は淡紅白色から褐色で，頭髪はブロンド，暗褐色，黒色で波状あるいは巻毛である。目は大きく，虹彩は緑色，褐色，黒色と変化に富んでいる。頭の形は，前後径の長い長頭と短い短頭がある。鼻は高く，幅は狭い。そのため鼻孔は前後に細長い。身長は中等度か高い。
（2）モンゴロイド 皮膚の色は淡黄色から褐色で，毛は少なく，ひげはうすい。短頭で，頭髪は直毛，虹彩は黒色ないし濃褐色である。鼻は中等度ないし低い。内眼角に蒙古ひだをみることがある。身長は中等度ないし低い。新生児，幼児の臀部の皮膚に青色の蒙古斑があることが多い。
（3）ニグロイド 皮膚は濃褐色ないし赤褐色，黒色で，体毛はわずかである。長頭で虹彩は黒い。鼻は低く，幅が広い。くちびるは厚く，外方へ突出翻転している。身長はさまざまである。
体型habitは，E.クレッチマーによって，次の3群に類型化されている。（1）細長型 体つきはきゃしゃで，体重は軽い。顔は細長く，鼻はとがっている。胸は薄く，扁平で，上下に長い。皮膚は乾燥し，顔色は青白く，貧血性である。（2）闘士型 男性は皮下脂肪は少なく，筋骨がたくましく，肩幅は広く，腹はひきしまっている。胴は逆三角形を呈し，女性は皮下脂肪が発達していることも多い。（3）肥満型 皮下脂肪は多く，筋肉の発達は中等度で，四肢の発達はよくない。頸は短く，かつ太い。顔は丸みを帯び，腹は膨大し，突出している。
これら体型は遺伝的，体質的な素因に栄養状態や疾病などの環境要因の影響を受けてできたもので，精神活動や特定の疾患の罹患性に関係していることも多いことから，今日でも臨床的に利用されている。
体の働きは，多くの器官で分担される。それぞれの器官の働きは，互いに協調し合い，統合される。器官は，その働きのうえから，植物性器官と動物性器官に分類される。植物性器官は，消化器，呼吸器，循環器，内分泌器，生体防御器官，生殖器，排出器に分けられ，体の代謝，免疫，種の保存などに関与する。これらの器官は，ほとんどが頭部の前下面，および体幹の腹側に集められている。一方，動物性器官は，感覚器，運動器，神経系で，頭部と体幹背側，四肢の大部分を占める。
体は，いくつかの器官を介して，外部環境に開かれている。食物を摂取する消化器，外界の酸素をとり入れ，体のなかで生じた炭酸ガスと交換する呼吸器，さまざまの外界の刺激を受容する感覚器，外界から侵入する異物に対して防衛作用を担う免疫機構，代謝の過程で生じた遺残物を体外に排出する排出器などである。
口から摂取された食物は，まず歯によって咀嚼（そしやく）され，食道や胃などの消化管を通過する間に，さらに機械的に破砕されながら，消化管に付属する多数の腺から分泌する消化酵素によって分解され，小腸や大腸の腸壁から吸収される。消化作用とは，食物それぞれの特異的な物質をいったん非特異な低分子化合物に分解し吸収することで，体はその低分子を素材として，体に特異的な化合物に再合成する。腸管で消化を受けた残りの難溶性の物質は直腸を経て肛門から排出される。
体が食物として摂取するおもな栄養素は，糖質，タンパク質および脂質である。糖質としては，デンプンが大部分を占めるが，これが加水分解されてブドウ糖になって吸収される。ブドウ糖は体の重要なエネルギー源で，その一部はグリコーゲンとなって肝臓や筋肉に備蓄される。食物中のタンパク質は，体を構成するタンパク質の合成に利用される。脂肪は最も効率のよいエネルギー源で，同一量の糖質やタンパク質の2倍以上のエネルギーを産生する。三大栄養素の代謝過程で遊離したエネルギーは，体を構成する細胞が機能を営むうえで必要とする動力源である。その残余のエネルギーは熱に転換され，体温の維持に利用される。とくにタンパク質の代謝から得られたエネルギーは，寒冷時に体を温める熱の発生に関与している。
体のなかで最大の産熱器官は骨格筋で，安静時においても全熱量の75%を占める。そのほか産熱作用の顕著な器官ないし組織は，肝臓と，ヒトの体では，うなじ，側胸部，肩甲部の皮下に分布する黄色脂肪組織である。
体のなかで栄養素の代謝によって発生したエネルギーが消費される場合，酸素の供給を必要とし，その作用の結果，炭酸ガスが生じる。これらガスの効果的な交換は，呼吸器とくに肺と血液，さらに血液を肺から体のすみずみにまで循環させる循環器によってなされている。呼吸器の主役は左右の肺と，そのなかへ空気を送り込む気道，すなわち鼻腔，喉頭，および気管，気管支である。左右の肺は陰圧の胸腔のなかに収められており，吸気時に胸腔が前後上下に拡大すると，空気は気道から勢いよく肺内へ流入する。両肺は7億5000万個の肺胞という小室に仕切られ，その小室間の薄い壁には毛細血管の網が埋め込まれている。その壁を介して肺胞腔と血液との間でガス交換が行われる。肺胞壁の総面積は50～100m2で，体の外表の50～60倍の広さに達し，いかにガス交換の場が広大であるかがわかる。
→呼吸
肺胞で酸素を受け渡された血液は，循環系を経て体のすみずみにまで運ばれる。循環系は，ポンプ作用を行う心臓を中心として，二つの循環路の血管系，すなわち肺循環（小循環）と体循環（大循環）からなる。血液は数種の細胞（血球）と液性成分（血漿）からなる。血液によって輸送される物質には，酸素や炭酸ガス以外にも，消化管から吸収した栄養素や，内分泌腺から放出されたホルモン，代謝産物などがある。さらに血液は，体液の浸透圧や水素イオン濃度の調整，体液の組成の均等化や体温の均一化にも関与している。循環系には血管系のほかにリンパ系がある。リンパ管のなかを流れるリンパ液は，血液の液性成分が血管から組織中へ滲出し，組織間隙を満たしたのち，開放したリンパ管へ吸い上げられた液体で，細胞成分としてはリンパ球を含み，リンパ本管，胸管を経て再び血管中に回収される。リンパ液は吸収した脂肪をカイロミクロンchylomicron（乳状脂粒）として輸送する。血液やリンパ液，さらに細胞や組織間隙を満たす液性成分は体液と呼ばれ，その重量は体重のほぼ60%を占めている（なお，体液という場合に，細胞内液を除いた液性成分をさすこともある）。
体には，内外の環境変化を情報として受容し，それに対して鋭敏かつ適切に対処する系統が存在する。その系統には，（1）受容－運動系，（2）受容－分泌系，（3）生体防御系がある。（1）と（2）は，刺激を特殊に分化した感覚細胞で受容し，その興奮を直接，あるいは神経系を介して筋肉や腺の効果器に伝達する機構である。（3）は，外界から，体にとっては異種の，すなわち非自己の物質の侵入を受け，それが抗原刺激となり，その抗原に特異的な抗体を産生する応答機構であり，免疫と呼ばれる。（1）～（3）のいずれの応答も，外界へ開かれた体がその独立性を発揮する現象で，体の内部環境の恒常性を維持する重要な機能である。
（1）感覚器官 光を受容する視覚器や，音の振動を受容する聴覚器のように刺激が物理的因子によってなされる感覚器と，味覚器，嗅覚（きゆうかく）器や，内部環境を検知する血液ガスの情報受容器のように化学的刺激を受容する感覚器がある。受容器と効果器（筋肉や腺）の間には，興奮を伝達する神経系が介在していることが多い。しかし，受容器の興奮を神経系を介して伝達するという図式は，すべてに当てはまるわけではない。ある種の消化管ホルモンを分泌する腸管の細胞は，腸管内の化学刺激を受容すると，その細胞自身が上皮下の血管内へ向かってホルモンを分泌する。このような細胞は，感覚細胞と内分泌細胞の両者の性質を兼ね備えており，受容分泌細胞と呼ばれる。このほか，嗅覚をつかさどる嗅上皮のように，神経細胞とも感覚細胞ともつかない細胞（通常，神経細胞のなかに分類されているが）がにおいの分子を受容すると同時に，その長い突起によって興奮を脳へ伝達している。また神経細胞自身によって産生されたホルモンが，その細胞の長い突起（神経突起）のなかを流れ，突起の先端から血管へ放出されるようなものもある。このような分泌は神経分泌といい，脳下垂体後葉ホルモンなどの分泌の形式にみられる。なお，〈視覚〉〈聴覚〉〈嗅覚〉〈味覚〉〈触覚〉などの感覚の詳細については，各項を参照されたい。
（2）神経と脳 神経系の主役を演ずる細胞は，通常長く分岐をくりかえす複雑な突起をもつ神経細胞で，ニューロンとも呼ばれる。脳では，多数のニューロンが互いにシナプスという結合を行い，長くかつ込み入ったニューロンの連鎖をつくる。この連鎖の簡単な例は，脊髄反射にみるような反射路で，受容器の興奮をインパルスという電気信号におき換え，少数のニューロンを介して効果器に伝える。第2はインパルスを統合し，調節作用や，適応を行う統合器としてのニューロン連鎖である。この連鎖にはより多くのニューロンが関与し，脳幹や大脳辺縁系にある旧皮質が中枢となる。生命維持や種の保存に必要な本能は，この連鎖によってなされる。第3は受容器から送られてきたインパルスを蓄積させ，それらを組み合わせ，新しい行動を創造するなど，最も高等な精神活動を行うニューロン連鎖で，ヒトではとくによく発達している。その中枢は大脳の前頭葉に存在する。
→脳
（3）脳と内分泌 情報を統合する脳は，また内分泌器官とも密接な連係を保っている。その代表的な連係は脳の底部にある視床下部-脳下垂体系を介して行われるが，このとき視床下部において神経情報が液性情報へ転換される。脳下垂体前葉は生命維持や種族の保存に重要な役割をもつ副腎皮質，甲状腺，生殖腺などの下位の内分泌器官に対して，血流を介して刺激ホルモンを放出する。この脳下垂体前葉は，より高位の視床下部から放出されるそれぞれの調節ホルモンによって制御されている。脳下垂体前葉からは，このほか，糖や脂質の代謝や骨の成長にたいせつな成長ホルモンを分泌する。
→ホルモン
体の多くの活動は体に内蔵されている生物時計の支配下におかれ，25時間に近い周期をもっている。この周期は概日リズム，または日周リズムと呼ばれる。そのリズムは生後8週に完成する。生物時計の一つは，視床下部にある視交叉（こうさ）上核と呼ばれる神経細胞に存在する。これら一群の神経細胞は，内因的に夜間活発にインパルスを発し，昼間は活動を休止している。視交叉上核から出た神経繊維はいくつかのニューロン連鎖ののち交感神経の上頸神経節に達し，その節後繊維は松果体に分布する。これら交感神経は夜間興奮して多量のノルアドレナリンを放出するが，それによって松果体細胞のメラトニン代謝に関与する酵素の一つ，N-アセチルトランスフェラーゼの生成が促進される結果，松果体は夜間多量のメラトニンを産生放出する。メラトニンは性腺の発達に対して抑制的に働くといわれる。生物時計はこのように体がみずから備えている内因性の時計機構であるが，この時計はつねに外界の明暗，すなわち太陽からの光刺激によって補強されているので，光・神経・内分泌系といわれる。ここにも体と外部環境との密接な関係をうかがい知ることができよう。
体の内部環境は，つねに外界からの影響下にさらされているが，その恒常性を維持するもう一つの機構は，生体防御系すなわち免疫系である。免疫応答は，体にとって異種の物質（抗原）が体に侵入することによって起こる。体は非自己と自己の要素を識別し，その情報を免疫担当細胞へ送る。免疫担当細胞には，リンパ球，顆粒球，単球などの血液細胞と，組織内に居住するマクロファージなどが含まれるが，これらの細胞は，いずれも骨髄の幹細胞から分化したものである。体は〈免疫監視機構〉と呼ばれる機構を備え，つねに外敵の侵入や体の内部に生じた異質，例えば癌細胞の発生などに対して監視している。体の免疫応答が乱れると，さまざまの反応や疾患が生じる。例えばアレルギーは，体にとって保護的に働くべき免疫応答が，かえって体には悪い影響を及ぼす現象である。また自己免疫疾患は，自己の体の構成成分に対して，自己の抗体産生細胞が産生した抗体が反応することによってひき起こされる疾病である。
→免疫
以上述べてきたように，体は食物を摂取し，エネルギーを産生し，内部環境の恒常性を維持しつつ，さまざまの機能を遂行しているが，やがてそこには死が訪れる。われわれの体はヒトに固有な寿命をもっている。寿命を規定している要因の一つに細胞の老化が挙げられる。細胞が老化すると，核酸の合成能が抑制され，核酸やタンパク質に生じた傷害に対してその修復能が減退する。また酵素の安定性も減弱する。結合組織の主要なタンパク質であるコラーゲンは，老化によって分子間架橋が増加し，固くもろくなる。そのために血管や組織の弾力性が弱まり，ひいては血流抵抗が増大し，二次的に細胞機能が減退するという悪循環が生じる。老化の機序は，なお明らかにされていないが，遺伝的要因と，体に傷害的に働く環境因子の蓄積が考えられている。
執筆者：和気 健二郎
身体についての見方は，西洋と東洋ではかなり違っている。〈身体〉をあらわすヨーロッパ語（英語body，フランス語corps，ドイツ語Körperなど）は，同時に生命のない〈物体〉をも意味しており，身体は物体の一種であると考えられてきた。つまり西洋の伝統では，〈物〉と〈心〉をはっきり分ける二元論の考え方が強い。二元論のもとになったのはユダヤ教とキリスト教の考え方である。ユダヤ思想では霊（ルーアハrûaḥ）と肉（バーサールbāśār）をはっきり分けたが，この霊肉二元論がキリスト教に受けつがれ，さらに近代の物心二元論が発展してきた。古代ギリシアでは，心と身体・物体の分け方はもっと複雑である。
これに対して東洋では，身体と物体は同じものではない。〈身〉という漢字は女性がみごもった形を示す象形文字である。一方，〈体（体）〉は身体，四肢，形，姿などを示す文字であるとともに，物事の理（ことわり），本質（もと），道（すじみち）といった精神的意味をも含んでいる。〈心〉は元来心臓の形を示す文字であるが，心のありかが心臓にあると考えられたので〈こころ〉を意味する文字になったのである。したがって〈心〉も元来は身体から分けられない。つまり東洋の伝統では，身体は精神と物質の中間にあって，両方を一つに結びつけているものであった。西洋のようにはっきりした物心二元論が発達しなかったのはこのためであろう。古代インドでは，身体を意味する言葉は〈カーヤkāya〉と〈シャリーラśarīra〉の二つがあるが，カーヤは要素の集まり，シャリーラは〈生体〉ないし〈死体〉の意味である。
近代に入って，身体の見方に大きな影響力をもったのはデカルトの物心二元論である。キリスト教の霊肉二元論には，道徳的判断，つまり肉体を罪の源泉とし，霊魂のみが神に通ずるとする見方があったが，デカルトの二元論は道徳的判断をとり払って，理論的見地から物質と精神を分けている。近代の科学と哲学はここから出発する。科学は，物体と身体は心とまったく無関係な物質的メカニズムであるとみる。また哲学は，精神の本質を理性に求め，身体と関係の深い感覚や感情・本能などをしりぞけた。ここに近代合理主義の人間観が成立する。このような考え方は，肉体を罪深いものとするキリスト教の人間観を否定し，性を解放する力になったともいえるが，二元論そのものは残っている。近代における性の解放は，一面では物としての肉体の解放つまり性欲の解放であって，そこでは性はなんら精神的意味をもたない生物的本能とみなされているといえるかもしれない。このように，近代科学は心と身体・物体をはっきり区別するので，近代の医学も，心と無関係な身体の生理的組織や機能だけを研究するのが主流になった。基本的に病気は身体組織の異変であるから，手術や薬物の作用によってそれをとり除くことが治療であると考えられたのである。
このような近代の身体観に対して，現代では，しだいに反省が起こってきている。ニーチェは近代合理主義の人間観を批判し，〈近代人は身体の重要性を忘れている〉と主張した。彼の考え方は，S.フロイトの深層心理学の先駆である。フロイトは，神経症やヒステリーが生理的原因によって起こる病気ではなく，無意識のコンプレクスによって起こることを発見し，心身の相関性を明らかにした。ユングはフロイトの影響を受けながらも，その性欲説を批判し，性は単なる生物的本能を意味するにとどまらず，無意識に潜在する深い精神的要求，たとえば芸術や宗教の問題と関係があることを明らかにした。フロイトやユングの考え方は最初強い非難を受け，精神医学者の一部に受けいれられたにすぎなかった。しかし，1950年代以降生理心理学の研究が進み，とくに大脳の〈旧皮質〉や自律神経の作用と情動作用の関係が明らかになってから，深層心理学の臨床上の知識が神経生理学の立場から証明されるようになった。さらにパブロフ以来の条件反射学の成果とも関係する領域が多くなり，心身相関のメカニズムを研究する心身医学，あるいはホーリスティック医学（全体医学）という研究分野も生まれてきた。つまり，心と身体を一体不可分のものとしてとらえる見方は，精神医学という特殊な一分野だけの見方ではなくて，内科学をはじめ臨床医学の全分野にかかわる問題となり，近代医学の身体観があらためて問い直されるようになってきたのである。
科学の領域にみられるこのような動向の背景には，現代における社会状況の変化が反映している。社会の管理化が進み，変化のテンポが激しくなってくるにつれて，社会の圧力が人間の心にゆがみをもたらし，神経症，心身症，自律神経失調症といった心身相関性の強い病気が，いわば〈時代の病気〉といえるほど，著しく増加してきた。また企業の営利主義から生まれた薬害が目だつようになり，人間不在の医療や心を切り捨てた身体観に対する不信が高まり，身体についての新しい見方が要求されてきているといえよう。哲学の分野でも，ベルグソンやメルロー・ポンティのように，心理学や精神病理学の研究に注目しながら，心身の相関関係について分析し，デカルト以来の物心二元論を克服しようとする動きがみられる。実存哲学や現象学も，身体の問題の重要性に注目するようになった。哲学の世界にみられるこのような動きは，近代医学の前提にあった合理主義的人間観，つまり身体と関係の深い本能や情動の役割を無視し，理性にのみ信頼をおいてきた考え方に対して反省を加えようとするものであるといえる。
ここで注目されるのは，上述のような動向にともなって，東洋思想の伝統の中にある身体観や人間観がしだいに注目されるようになってきたことである。初めにいったように，東洋では精神と物質，あるいは心と身体をはっきり区別する二元論の考え方はなかった。その基礎には，東洋の宗教の修行法や東洋医学の考え方がある。たとえば，禅やヨーガや道教などの瞑想（めいそう）法や修行法は，心の働きと身体の働きが一体になった〈心身一如〉の境地を理想として追求している。また東洋医学の考え方は宗教と関係が深い。インド医学（アーユル・ベーダ）はヨーガの哲学と関係が深く，中国医学の鍼灸（しんきゆう）療法は道教との関係が深いものである。このような東洋思想の価値にいち早く注目したのは，ユングやフロムのような精神医学者たちであった。彼らは，禅やヨーガや道教の修行法の中に，現代の深層心理学や精神医学が追求しつつある問題と同じテーマが，古くからとりあげられてきたことに注目した。今日の心身医学では，禅やヨーガの方法からヒントを得た心理治療の方法を用いることも多くなっており，東洋医学の身体観について，現代の生理心理学の見地からその意味を明らかにしようとする研究もしだいに盛んになってきている。このような動きは，アメリカをはじめとする欧米諸国で起こったものであるが，日本でも，近年ヨーガや東洋医学に対する関心がしだいに高まってきた。
身体論は哲学や医学ばかりでなく，宗教，芸術（とくに演劇），スポーツなどといったさまざまの領域とも関係が深い。現代演劇の動向には，知的観念では十分に表現できない人間の情念の深層にあるものを，身体表現（パフォーマンス）によってとらえようとする考え方があるといえよう。またスポーツでは，柔道，空手，合気道といった武道が欧米に注目されるようになっていることも，一つの動きとして注目される。一般的にいえば，現代の世界には，言語表現に対する不信感ともいうべき傾向がみられる。政治の世界におけるイデオロギー不信の傾向などは，そのいちじるしい例である。そこには，言語による知的表現の底にかくされた身体的情念の意味を，あらためて問い直そうという模索の姿勢がみられるといってよいであろう。現代における身体論は，その意味において，近代的人間観を克服する大きな契機をはらんでいる。
→心 →心身問題
執筆者：湯浅 泰雄
有理数全体，実数全体，複素数全体のように四則演算が（0で割ることを除外して）できる体系を体という。このような体系が意識されるようになったのは，方程式の代数的解法の研究に伴って，一つの代数方程式の根の全体，または一部についての整式で表される数の体系が扱われるようになったことによる（ガロアの理論）。やがてJ.W.R.デデキントが体の概念を定義し，ガロア群を根の置換としてでなく，体の自己同型として考察した。L.クロネッカーは体Kの有限次代数拡大体を，多項式環K［x］の既約多項式f（x）によって，剰余類環K［x］/f（x）K［x］の形で与える考えを導入した。また古くから整数の扱いにあった〈pを法とする合同〉によって，p（素数）個の元からなる体も考察の対象になり，またヘンゼルK.Hensel（1861-1941）のp進数の登場などにより，シュタイニッツE.Steinitz（1871-1928）が，素体，分離代数的元，完全体などの概念の導入を含めて，体の理論を一つのまとまった形にした。その後，無限次の代数拡大や超越拡大などの理論がさらに整備された。
環の定義に似ているが，それより強い条件で次のように定義する。
集合Kに二つの演算（ふつう，加法，乗法と呼ぶ）が定義されているものとする。すなわち，Kの元a，bに対して，その和a＋b，積abが定まって，それらはKの元である。この演算について，次の条件（1）～（3）が満たされるとき，Kは体であるという。
（1）Kは加法に関して可換群をなす。すなわち，（a）a＋b＝b＋a，（b）（a＋b）＋c＝a＋（b＋c），（c）零元0が存在して，a＋0＝a＝（0＋a），また各元aに対して，a＋b＝0となる元bが存在する。このようなbはただ一つであり，－aで表される。
（2）Kの0以外の元全体K＊は乗法に関して可換群をなす。すなわち，（a）ab＝ba，（b）a（bc）＝（ab）c，（c）単位元1が存在して，a1＝aであり，各aに対してab＝1となる元bがある。このbはaの逆元と呼ばれ，a⁻1で表される。
（3）加法と乗法の間に分配法則が成り立つ。
a（b＋c）＝ab＋ac
（b＋c）a＝ba＋ca
（2）でK＊を単に群としたものを斜体というが，斜体をも含めて体と呼ぶことがある。その場合は上の定義のものを可換体と呼ぶ。斜体であって可換体でないものは非可換体と呼ばれる。四元数体はその例である。
なお，体という語はドイツ語のKörperの訳語として導入されたものである。フランス語も同義のcorpsであるが，英語はfieldである。
体Kから体Lへの写像fがあって，f（a＋b）＝f（a）＋f（b），f（ab）＝f（a）f（b），f（K）＝Lであるとき，fはKからLへの同型であるという。さらに，K＝Lであるとき，fはKの自己同型であるという。
aが体Kの元でnが自然数のとき，naはaをn回加えた和a＋a＋……＋aを表す。また，（－n）aは－（na）と定める。すると，Kの単位元1に対して，m1＝0となる整数m全体を取ると，（1）0だけであるか，（2）ある素数pの倍数全体であるかのいずれかである。（1）のとき0を，（2）のときpをKの標数と定める。
有理数全体，実数全体，複素数全体はいずれも体である。これらを有理数体，実数体，複素数体と呼ぶ。pが素数で，Zが有理整数環であるとき，剰余類環Z/pZはp個の元からなる体である。
体Kの含む最小の体をKの素体という。標数0なら有理数体と同型であり，標数p≠0なら上記Z/pZと同型である。
体Kが体Lに含まれるとき，KはLの部分体，LはKの拡大体であるという。体MがKの拡大体であり，Lの部分体であるとき，MはKとLの中間体であるという。
a1，a2，……，amがLの元であるとき，Kとa1，a2，……，amを含む最小の体がある。これをKにa1，a2，……，amをつけ加えた体，またはK上a1，a2，……，amで生成された体といって，K（a1，a2，……，am）で表す。Lの元aに対して，Kに係数をもつ多項式f（x）＝xn＋c1xn⁻1＋……＋c2xn⁻2＋……＋cn（n≧1）のうち，f（a）＝0となるものがあれば，aはK上代数的であるといい，そうでないとき超越的であるという。またこのとき，このようなf（x）のうち次数nが最小のものをaの最小多項式という。Lの元がすべてK上代数的であるとき，LはKの代数拡大であるといい，そうでないとき超越拡大であるという。LをK-加群とみて，n個の元からなる一次独立基をもつとき，LはKのn次の拡大であるといい，また，nをこの拡大の次数と呼び，［L：K］，（L/K）などの記号で表す。この場合，LはK上代数的である。また，Mが中間体であれば，［L：K］＝［L：M］×［M：K］。有限次でない代数拡大を無限次代数拡大という。
体Kの拡大体Lの元t1，t2，……，tnについて，Kに係数をもつn変数の多項式f（x1，……，xn）で，f（t1，……，tn）＝0となるものは定数0以外に存在しないとき，t1，……，tnはK上代数的独立であるという。このようなt1，……，tnで，LがK（t1，……，tn）上代数的であるとき，t1，……，tnはK上Lの超越基であるといい，tiの数nをLのK上の超越次数と呼ぶ。Mが中間体であれば，（LのM上の超越次数）＋（MのK上の超越次数）がLのK上の超越次数と一致する。
複素数体の部分体を数体という。また，有理数体上有限次の数体を（有限次）代数体と呼ぶ。
Lが体Kの代数拡大体であるとき，Lの元aについて，aのK上の最小多項式f（x）が重根をもたない（この場合，f（x）は既約であるので，導関数が定数0ではないという条件と同値になる）とき，aはK上分離的であるという。K上分離的なLの元全体は中間体になる。これをLにおけるKの分離閉包という。Lの元がすべてK上分離的であるとき，LはKの分離（代数）拡大であるという。分離（的）でないことを，非分離（的）という。代数拡大体がすべて分離的である体を完全体という。標数0の体はすべて完全体である。
Fが体Kの超越拡大体であるとき，FのK上の超越基t1，……，tnについて，FがK（t1，……，tn）上分離的であるとき，t1，……，tnはFのK上の分離超越基と呼ぶ。このようなものが存在するとき，FはK上分離的，または分離生成であるという。FがK上有限個の元では生成されない場合を含めての定義は，Kの任意の拡大体Lについて，テンソル積F⊗kLがべき零元をもたないという条件でなされる。
元の数が有限である体を有限体という。ガロアが最初に考えたとの理由で，ガロア体とも呼ばれる。標数pの有限体Fの，素体Z/pZ上の次数がnであれば，Fの元数はpnである。逆に，素数pのべきq＝pnを与えれば，元数qの体Fは存在し，同型の意味でただ一つであり，また，それはXq－Xの根全体の集合である。さらにFの乗法群は位数q－1＝pn－1の巡回群をなす。
他方，元の数が有限の斜体は必ず可換体であることが知られている。
複素数体のように，代数拡大体は自身に限るような体を代数的閉体という。体Kが代数的閉体であるための条件は，K上の1変数の多項式xn＋c1xn⁻1＋……＋cn（n≧1）は必ずKの元α1，……，αnによって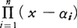
と一次因子の積に因数分解することである。
体Lの代数拡大体で代数的閉体であるものをLの代数的閉包という。これは存在して，同型の意味で一意的であることが知られている。
実数体のように，体Kに全順序が与えられていて，（1）a＞bならば，a＋c＞b＋c，（2）a＞bかつc＞0ならば，ac＞bcの成り立つとき，Kは順序体であるという。このとき，a＞bならば－a＜－bである。
体Lにおいて，－1が平方元の和に決してならないとき，いいかえれば，どのような自然数nを取っても，x12＋x22＋……＋xn2＋1＝0がKの中で解をもたないとき，Lは実体であるという。順序体は実体であり，逆に実体に適当な順序を与えて順序体にすることができる。
執筆者：永田 雅宜
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
可換環Kの零元以外の元全体が乗法で群になるとき、Kを体という。体においては、足し算、引き算、掛け算、割り算の四則演算ができる。有理数全体Q、実数全体R、複素数全体Cは、普通の数の四則で体になる。それぞれ有理数体、実数体、複素数体という。体は、零元と異なる単位元をもち、零因子のない可換環、つまり整域である。整数全体Zは整域であるが体でないように、整域は体と異なるが、整数環Zから分数をつくって有理数体Qを構成するように、任意の整域Aから、Aの商体といわれる体
K=｛a/b|a,b∈A,b≠0｝
がつくれる。たとえば、体k係数の多項式全体の整域k［X］の商体は、k上の有理関数体
k(X)=｛f(X)/g(X)|f(X),
g(X)∈k［X］,g(X)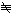
0｝
である。
単位元をもつ可換環Aのイデアルɑによる剰余環A/ɑ=｛a+ɑ|a∈A｝に対して、
A/ɑ:体
⇔ɑ:Aの極大イデアル
が成り立つ。この性質を用いて体をつくることができる。たとえば、ある素数pで割り切れる整数全体Z・pは整数環Zの極大イデアルであるから、剰余環Z/Z・pは体になる。この体Z/Z・pはp個の元
0+Z・p,1+Z・p,
……,(p-1)+Z・p
からなっている。このように有限個の元からなる体を有限体といい、Q、R、Cのように無限個の元をもつ体を無限体という。
体Kから体K′の上への一対一写像ρが
ρ(a+b)=ρ(a)+ρ(b),
ρ(ab)=ρ(a)ρ(b) (ab∈K)
を満たすとき、ρをKからK′の上への同形写像という。このとき、ρの逆写像ρ-1もK′からKの上への同形写像となり、二つの体K、K′は、体として同じ性質をもつ。このゆえに、KからK′の上への同形写像があるとき、体Kと体K′は同形であるという。
いまω=（-1+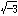
）/2をとり、Q係数の多項式f(X)にωを代入して得られる複素数f(ω)全体の集合をQ(ω)とする。この集合Q(ω)は、数の加法と乗法で整域になっていることはすぐわかるが、実は体である。実際、ωが多項式p(X)=X2+X+1の根であることに注意すると、多項式f(X)に対し、f(ω)≠0なら
a(X)f(X)+b(X)p(X)=1
を満たすa(X),b(X)∈Q［X］があるが、この式にX=ωを代入してf(ω)-1=a(ω)∈Q(ω)が示されるからである。さらに、体Q(ω)は、多項式環Q［X］の、p(X)で割り切れる多項式全体のつくる極大イデアルɑによるQ［X］/ɑに同形であり、Q(ω)の元は、a+bω(a,b∈Q)の形に一意的に書けることが知られている。前のωのように、零多項式でない有理数係数の多項式の根になっている複素数αを、一般に代数的数というが、このようなαに対し
Q(α)=
｛f(α)∈C|f(X)∈Q［X］｝
は、Q(ω)と同じようなQを含み、Cに含まれる体になる。このような体を代数数体という。
体kが体Kに含まれ、kの任意の元a、bの四則演算が、a、bをKの元とみなした四則演算に一致するとき、体kを体Kの部分体という。QはRの、RはCの部分体であり、前述のQ(α)はCの部分体である。体Kには、ただ一つの最小の部分体Fがある。Fは有理数体Qか、またはZ/Z・p（pはある素数）のいずれかに同形である。それぞれの場合に従って、Kの標数は0であり、またはpであるという。Q,R,C,Q(α)のような数の体の標数は0であり、(Z/Zp)(X)の標数はpである。標数pの体では、
p・a=0,
(a+b)p=ap+bp (a,b∈K)
が成り立ち、標数0の体とだいぶようすが違う。
体はデーデキントらによって、多項式の根を代数的に求める問題などに関連して考え出されたが、今日の代数学の重要な基本概念の一つになっている。
［菅野恒雄］
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
…透明性も水彩の特色の一つと考えられているが，これに増粘剤(膠（にかわ）)を混入すると不透明性が得られ，これをグアッシュと呼ぶ。またより重厚なマティエールを出すため，これに不透明な白色顔料(ボディbody)を加えることが多いので，不透明水彩をボディ･カラーと呼ぶこともある。また煤（すす）から作られるビスター，イカの墨から作るセピアで描いた単色画も水彩に近いものをもっている。…
…胴体，軀幹（くかん），体幹ともいう。頭，尾，付属肢，触角などの突出部を除く動物体の中心的な部分。普通は大きい塊をなし，内部に体腔をもち，そこにほとんどの内臓諸器官をおさめている。無脊椎動物では，胴といえる部分を識別できるのは節足動物だけであるが，胴の構成は分類群によって多少異なる。大半のグループでは胴は明りょうに分節した胸部と腹部からなるが，クモ類やカニ類では頭部と胸部が一体となって頭胸部をなし，それと腹部とが胴に相当する。…
…また栽培される作物は，このような周到な管理によって，はじめて量質ともにすぐれた収穫をあげうるような性質をもっている。古来，ヨーロッパ農業においては，集落近辺の農地を柵などで囲って園地gardenとし，ここで野菜や果樹の栽培を行うのが一般であり，外側の耕地fieldで行われる穀物栽培とは集約度という点で著しく異なり，このため，園耕と穀耕とがとくに区別されてきたのである。近代ヨーロッパにおける農村共同体の解体と，これと並行して進行した農業機械を中軸とする農業技術の発展は，農地の地割り制を変化させ，作物別の土地利用方式を一変させてきているが，園芸作物を中心とした集約的な農耕方式に対しては，依然，園耕という用語の使用される場合が少なくない。…
…一般には，空間そのものが何らかの作用(物理的，心理的)をもち，そこに現象を生じさせると考えられるとき，その空間を〈場〉と呼ぶ。場の概念は，必ずしも〈場〉と呼ばれない場合も含めて，今日，科学の諸領域で重要な役割を果たしつつある。それは，一つにはニュートン力学的な遠隔作用を前提とする力の概念に対抗して，またもう一つには原子論的発想に対抗して，とりあえずは19世紀に生まれた。したがって，出発点は物理学にあるといってよい。…
…〈はた〉とも読む。水田以外の耕地，すなわち水をたたえることなしに農作物を栽培する耕地をいう。水稲以外のほとんどの農作物は，水をたたえることなしに栽培するのが普通であるから，世界的にみて水稲作を行わない地域では，耕地はすなわち畑を意味する。水稲作を農業の根幹としてきた日本では，灌漑の可能な耕地のほとんどは，水田として造成されてきた経緯があり，土地登記上の地目としても，統計上の取扱いにしても，水田と畑は明確に区別されている。…
…また，二つの自然数の和，積は自然数であるが，29－33のように，差はかならずしも自然数とはならず，自然数の範囲内では減法も可能とは限らない。一般に，四則演算が可能な集合を体という。上の例では，有理数の集合，実数の集合や複素数の集合は体であるが，整数の集合や自然数の集合は体ではない。…
※「体」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
血液中の脂質（トリグリセリド、コレステロールなど）濃度が基準値の範囲内にない状態（脂質異常症）に対し用いられる薬剤。スタチン（HMG-CoA還元酵素阻害薬）、PCSK9阻害薬、MTP阻害薬、レジン（陰...
4/12 日本大百科全書(ニッポニカ)を更新
4/12 デジタル大辞泉を更新
4/12 デジタル大辞泉プラスを更新
3/11 日本大百科全書(ニッポニカ)を更新
2/13 日本大百科全書(ニッポニカ)を更新
