ひずみ（英語表記）strain

日本大百科全書(ニッポニカ)

ひずみ
strain
deformation

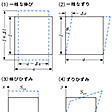
物体の変形の割合をひずみという。たとえば図の(1)のように物体の長さlをΔlだけ伸ばしたとき、Δl/lは伸びのひずみである。図の(1)の場合、幅aがΔaだけ縮むが、Δa/aも負の伸びのひずみである。また図の(2)のように物体を変形させた場合、これをずりといい、Δa/a（ほぼ角度θに等しい）をずりのひずみという。

　図の(1)、(2)のように物体が一様に変形したときは、外形の変化でひずみを表すこともできるが、一般にはひずみは物体内部の各場所で次のように定義する。物体中の1点Aが物体の変形によってA'まで変位したとしよう。もしこの変位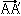が物体のあらゆる場所で同じならば、これは単に物体全体が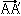だけ平行移動したことを意味し、物体はひずんでいない。ひずみがあるためには、物体の中の点の変位が物体の中の場所によって違っていることが必要である。変位も場所もともにベクトルで表されるから、ひずみ、すなわち変位の場所による変化は2階のテンソルで表される。物体の全体としての回転もまたひずみとは関係がないことを考えると、ひずみSは次のように2階のテンソルとして表される。

すなわち、ひずみテンソルは6個の独立な成分をもち、そのうちS_xx,S_yy,S_zzは伸びひずみを表し、S_xy,S_yz,S_zxは、ずりひずみを表す。図の(3)、(4)にS_xx,S_yzを示す。伸びひずみは体積の変化を伴うが、ずりひずみはそれを伴わない。

　S_xx＋S_yy＋S_zzが体積の変化の割合（体積ひずみ）を表す。すなわち、物体のある部分の体積vがΔvだけ増すとき、その部分のひずみを用いて
　　体積ひずみ＝Δv/v＝S_xx＋S_yy＋S_zz
と表される。

［和田八三久・西　敏夫］

ひずみ〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

ひずみ
strain

物体に外力が作用すれば変形が生じる。この変形の度合いを表すために，変形量ともとの基準量との比の値をひずみまたはひずみ度という。いま，物体内に微小な直方体要素を仮想し，変形があまり大きくないとすれば平行六面体状にゆがむ。微少変形の場合には直方体要素の一辺の長さ l₀ が lになったとした場合（l－l₀）/l₀を縦ひずみ（または垂直ひずみ）という。微少変形を考えるときには，力の釣合いは変形前の物体の形状について考えてよい。また，初めに直角をなす角からの増減を剪断ひずみという。直方体要素を物体内である特定の方向に選び出せば，直方体のまま伸縮して変形する。このときの縦ひずみを主ひずみといい，生じる方向と面をそれぞれひずみの主軸，主面と呼ぶ。等方・等質の物体では，応力の主軸，主面と一致する。なお，まれに変形量自体をひずみということもあるが，工学分野では通常用いない。

出典　ブリタニカ国際大百科事典 小項目事典